Zadanie nr 6307406

Ciąg 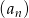(an) , gdzie 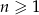n ≥ 1 dany jest wzorem rekurencyjnym

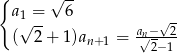
{ √ -- a√1 =- 6 √- ( 2+ 1 )an+1 = an√−--2 2− 1

Oblicz sumę 21 początkowych wyrazów tego ciągu.
Wyznacz wszystkie liczby naturalne , dla których spełniona jest nierówność
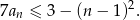
$2 7an ≤ 3 − (n − 1 ) .$

Rozwiązanie

Przekształćmy podany warunek rekurencyjny

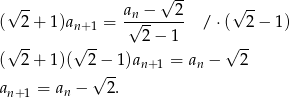
√ -- √ -- √ -- ( 2 + 1)an+ 1 = an√-−---2- / ⋅( 2− 1) 2− 1 √ -- √ -- √ -- ( 2 + 1)( 2√−-1)an+ 1 = an − 2 an+ 1 = an − 2.

Mamy więc do czynienia z ciągiem arytmetycznym, w którym 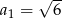a = √ 6- 1 i √ -- r = − 2 .

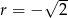Korzystamy ze wzoru na sumę początkowych wyrazów ciągu arytmetycznego.
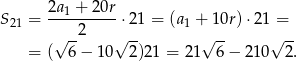
$2a1 +-20r- S 21 = 2 ⋅21 = (a1 + 10r) ⋅21 = √ -- √ -- √ -- √ -- = ( 6− 10 2)21 = 2 1 6− 210 2.$

Odpowiedź: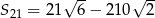
Ze wzoru na -ty wyraz ciągu arytmetycznego wiemy, że
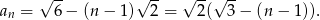
$√ -- √ -- √ --√ -- an = 6 − (n − 1) 2 = 2( 3− (n− 1)).$

Musimy więc rozwiązać nierówność

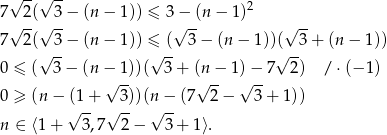
$√ --√ -- 7 2( 3 − (n − 1 )) ≤ 3− (n− 1)2 √ --√ -- √ -- √ -- 7 2(√ 3-− (n − 1 )) ≤√ (- 3− (n− 1))(√ -3+ (n − 1)) 0 ≤ ( 3 − (n − 1 ))( 3+ (n − 1)− 7 2) / ⋅(− 1) √ -- √ -- √ -- 0 ≥ (n − (1 + 3 ))(n − (7 2− 3+ 1)) √ -- √ -- √ -- n ∈ ⟨1 + 3,7 2− 3+ 1 ⟩.$

Ponieważ

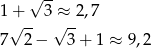
$√ -- 1√+-- 3√≈--2,7 7 2 − 3 + 1 ≈ 9,2$

otrzymujemy stąd .
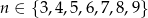Odpowiedź: