/Szkoła średnia/Ciągi/Rekurencyjny

Zadanie nr 7838839

Dodaj do ulubionych
Dodaj do rozwiązanych

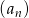Ciąg (an) określony jest rekurencyjnie: 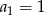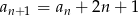a1 = 1 , an+1 = an + 2n + 1 dla n ≥ 1 .

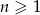  • Oblicz 4 wyraz ciągu (an) .
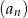  • Zbadaj monotoniczność ciągu (a ) n .

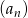Rozwiązanie

  • Liczymy
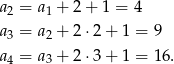
    a2 = a1 + 2+ 1 = 4 a = a + 2⋅2 + 1 = 9 3 2 a4 = a3 + 2⋅3 + 1 = 16.

     
    Odpowiedź: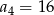 a4 = 16

  • Musimy zbadać jaki jest znak wyrażenia 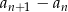an +1 − an . Jeżeli będzie dodatni to ciąg będzie rosnący, a jeżeli ujemny to malejący.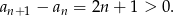
    an+1 − an = 2n + 1 > 0.

    Dany ciąg jest zatem rosnący.  
    Odpowiedź: Rosnący

Wersja PDF