/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna/Z liniową

Zadanie nr 6824854

Dana jest funkcja 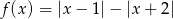f(x ) = |x− 1|− |x + 2| dla x ∈ R .

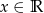  • Wyznacz zbiór wartości funkcji 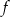f dla x ∈ (− ∞ ,− 2) .
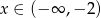  • Naszkicuj wykres tej funkcji.
  • Podaj jej miejsca zerowe.
  • Wyznacz wszystkie wartości parametru 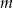m , dla których równanie 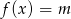f(x) = m nie ma rozwiązania.
Wersja PDF

Rozwiązanie

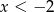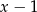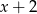  • Zauważmy, że dla x < − 2 oba wyrażenia x − 1 i x + 2 są ujemne. Możemy zatem opuścić wartości bezwzględne we wzorze funkcji zmieniając znaki tych wyrażeń na przeciwny: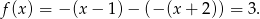
    f(x) = −(x − 1 )− (− (x + 2)) = 3.

    Ponieważ jest to funkcja stała, to zbiór jej wartości jest zbiorem jednoelementowym: {3} .  
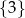    Odpowiedź: Zbiór wartości: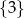 {3 } .

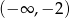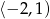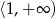  • Aby pozbyć się wartości bezwględnych we wzorze funkcji, musimy podzielić dziedzinę na trzy przedziały: (− ∞ ,− 2) , ⟨− 2,1) oraz ⟨1,+ ∞ ) . Z definicji wartości bezwględnej otrzymujemy: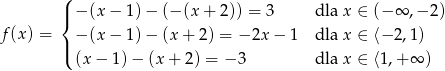
    ( |{ − (x − 1) − (− (x + 2)) = 3 dla x ∈ (− ∞ ,− 2) f(x ) = − (x − 1) − (x + 2) = − 2x − 1 dla x ∈ ⟨− 2,1) |( (x − 1) − (x + 2) = −3 dla x ∈ ⟨1,+ ∞ )

    Teraz bez trudu rysujemy wykres funkcji f .

    PIC
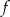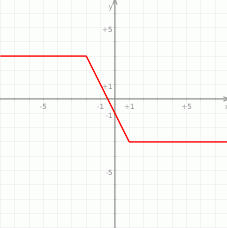
  • Korzystając z otrzymanego w b) wzoru (albo wykresu) widzimy, że funkcja ma tylko jedno miejsce zerowe i znajduje się ono w środkowym przedziale 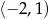⟨− 2,1) . Aby wyznaczyć je dokładnie rozwiązujemy równanie: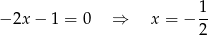
    1 − 2x − 1 = 0 ⇒ x = − -- 2

     
    Odpowiedź: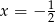 x = − 12

  • Z naszkicowanego wykresu (lub ze wzoru z punktu b) widać, że zbiór wartości funkcji 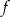f to przedział 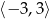⟨− 3,3⟩ . Zatem równanie 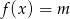f(x) = m ma rozwiązanie tylko dla 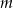m z tego przedziału. Odpowiedzią na zadane pytanie są zatem wszystkie pozostałe liczby.  
    Odpowiedź: R ∖ ⟨− 3,3⟩ = (− ∞ ,− 3)∪ (3,+ ∞ )
Wersja PDF