Zadanie nr 7875913
Dana jest funkcja 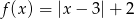 dla
dla 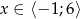 .
.
- zapisz wzór tej funkcji opuszczając symbol wartości bezwzględnej,
- naszkicuj wykres funkcji
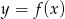 ,
, - naszkicuj wykres funkcji
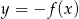 .
.
Rozwiązanie
Zauważmy, że 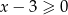 dla
dla 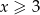 oraz
oraz 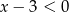 dla
dla 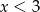 , zatem
, zatem
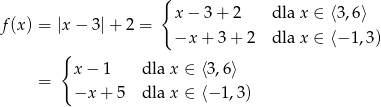
Teraz bez trudu szkicujemy wykres funkcji 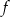 : dla
: dla 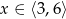 jest to kawałek prostej
jest to kawałek prostej 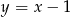 , a dla
, a dla 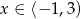 kawałek prostej
kawałek prostej 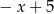 .
.
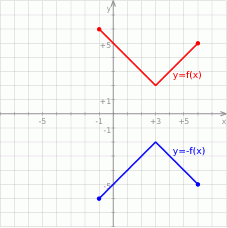
Wykres funkcji 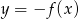 powstaje z wykresu
powstaje z wykresu 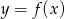 przez odbicie względem osi
przez odbicie względem osi 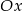 .
.
Odpowiedź: