Zadanie nr 8078911
Narysuj wykres funkcji 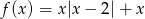 , gdzie
, gdzie 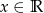 i na jego podstawie odpowiedź na pytania.
i na jego podstawie odpowiedź na pytania.
- Jaki jest zbiór wartości funkcji?
- Dla jakich argumentów wartość funkcji wynosi 2?
- W jakich przedziałach funkcja jest rosnąca?
- Czy funkcja jest parzysta?
Rozwiązanie
Zapiszmy wzór funkcji bez wartości bezwzględnej.
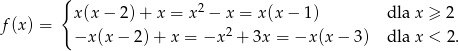
Teraz łatwo już naszkicować wykres funkcji 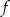 .
.
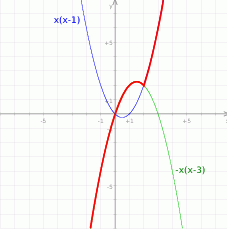
- Z wykresu odczytujemy, że zbiorem wartości jest
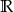 .
.
Odpowiedź: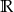
- Z wykresu łatwo zobaczyć, że są dwie takie wartości
 i łatwo je odgadnąć (i sprawdzić wstawiając do wzoru!):
i łatwo je odgadnąć (i sprawdzić wstawiając do wzoru!): 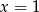 i
i 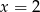 .
.
Odpowiedź: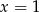 i
i 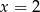
- Odczytujemy z wykresu:
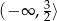 i
i 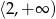 .
.
Odpowiedź: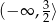 i
i 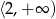
- Funkcja nie jest parzysta – wykres nie jest symetryczny względem osi
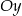 .
.
Odpowiedź: Nie, nie jest.

