/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna/Z liniową

Zadanie nr 9144881

Dodaj do ulubionych
Dodaj do rozwiązanych

Sporządź wykres funkcji 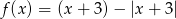f(x) = (x+ 3)− |x + 3| . Podaj miejsca zerowe funkcji, oraz przedziały monotoniczności.

Rozwiązanie

Zauważmy, że

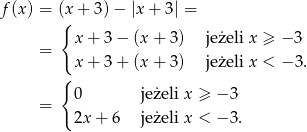
f(x) = (x+ 3)− |x + 3 | = { x + 3 − (x + 3) je żeli x ≥ − 3 = x + 3 + (x + 3) je żeli x < − 3. { = 0 jeżeli x ≥ − 3 2x + 6 jeżeli x < − 3.

Teraz bez trudu szkicujemy wykres funkcji.

PIC

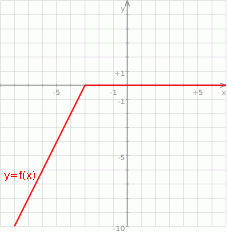
Z wykresu widać, że zbiorem miejsc zerowych funkcji 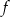f jest przedział 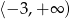⟨− 3,+ ∞ ) . Ponadto funkcja jest rosnąca na przedziale 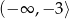(− ∞ ,− 3⟩ . Jest też niemalejąca na R .  
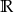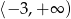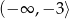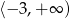Odpowiedź: Miejsca zerowe: ⟨− 3,+ ∞ ) , rosnąca na (−∞ ,− 3⟩ , stała na ⟨− 3,+ ∞ ) .

Wersja PDF