Zadanie nr 3434694
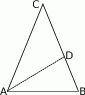
W trójkącie równoramiennym 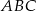 , w którym
, w którym 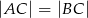 , poprowadzono dwusieczną
, poprowadzono dwusieczną 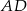 kąta przy wierzchołku
kąta przy wierzchołku 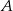 (patrz rysunek), przy czym
(patrz rysunek), przy czym 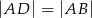 . Jaka jest miara kąta
. Jaka jest miara kąta 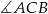 ?
?
A)  B)
B) 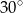 C)
C) 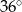 D)
D) 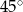 E)
E) 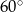
Rozwiązanie
Oznaczmy 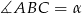 . Ponieważ trójkąt
. Ponieważ trójkąt 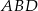 jest równoramienny, to
jest równoramienny, to 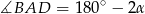 . Z drugiej strony, ponieważ trójkąt
. Z drugiej strony, ponieważ trójkąt 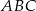 jest równoramienny i prosta
jest równoramienny i prosta 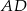 jest dwusieczną, kąt ten jest równy
jest dwusieczną, kąt ten jest równy 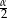 . Mamy zatem
. Mamy zatem
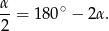
Daje to 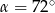 oraz
oraz
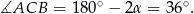
Odpowiedź: C

