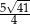/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 1074623

Dodaj do ulubionych
Dodaj do rozwiązanych

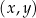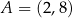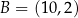W kartezjańskim układzie współrzędnych (x,y ) dane są punkty A = (2 ,8 ) oraz B = (10,2) . Symetralna odcinka 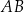AB przecina oś 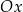Ox układu współrzędnych w punkcie 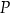P . Oblicz współrzędne punktu 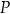P oraz długość odcinka AP .

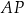Rozwiązanie

Napiszemy najpierw równanie symetralnej odcinka 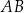AB . Można to zrobić na wiele różnych sposobów – my wykorzystamy definicję symetralnej jako zbioru punktów 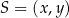S = (x,y) , które są równoodległe od końców tego odcinka.

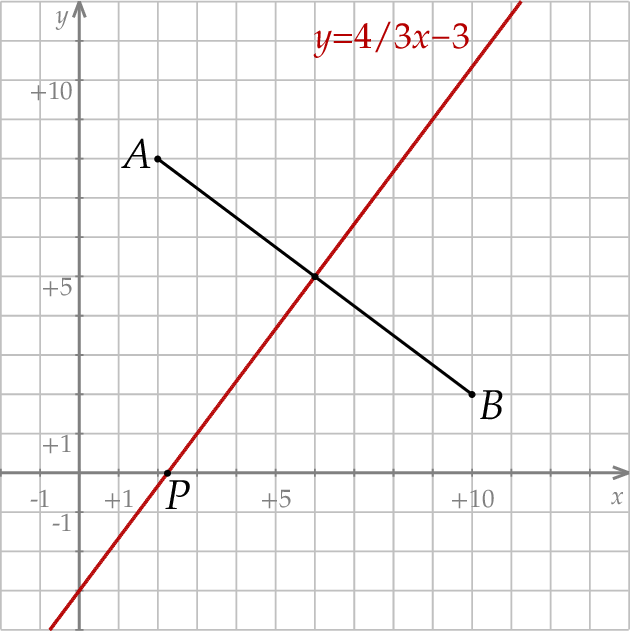
ZINFO-FIGURE

Mamy zatem

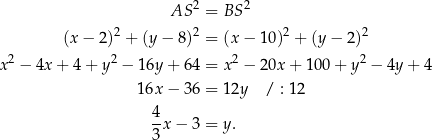
AS 2 = BS 2 2 2 2 2 (x − 2) + (y− 8) = (x − 10) + (y − 2) x2 − 4x + 4 + y2 − 16y + 64 = x2 − 20x + 10 0+ y2 − 4y+ 4 16x − 36 = 12y / : 12 4- 3 x− 3 = y.

Aby wyznaczyć punkt przecięcia tej prostej z osią 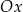Ox podstawiamy 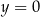y = 0 w tym równaniu.

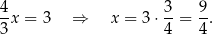
4-x = 3 ⇒ x = 3 ⋅ 3-= 9. 3 4 4

Zatem 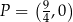( ) P = 94,0 i

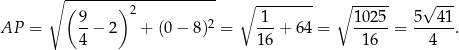
∘ (------)------------- ∘ -------- ∘ ------ √ --- 9 2 1 102 5 5 4 1 AP = --− 2 + (0 − 8)2 = ---+ 64 = ----- = ------. 4 16 16 4

 
Odpowiedź: √ -- 5--41 4

Wersja PDF