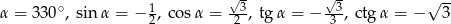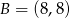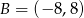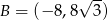Zadanie nr 1190331

Wyznacz wartości funkcji trygonometrycznych kąta 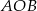AOB oraz jego miarę, jeżeli 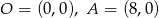O = (0,0), A = (8,0) oraz

Rozwiązanie

Rozpoczynamy od rysunku.

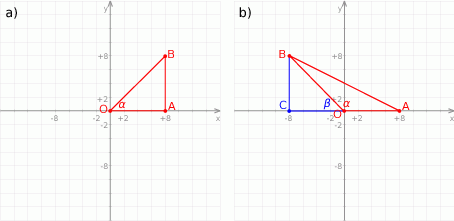
Z obrazka widać, że

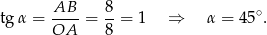
$-AB- 8- ∘ tg α = OA = 8 = 1 ⇒ α = 45 .$

Zatem

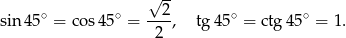
$√ -- sin45 ∘ = cos45 ∘ = --2, tg 45∘ = ctg 45∘ = 1. 2$

Odpowiedź: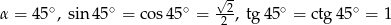
Jeżeli punkt 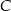jest rzutem punktu 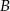na oś 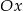to podobnie jak w poprzednim podpunkcie otrzymujemy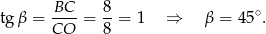
$BC 8 tg β = ----= --= 1 ⇒ β = 45∘. CO 8$

Zatem 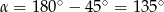oraz

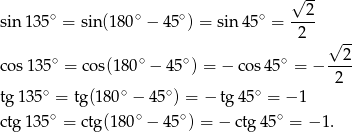
$-- √ 2 sin 135∘ = sin (180∘ − 45∘) = sin 45∘ = ---- 2 √ -- ∘ ∘ ∘ ∘ --2- cos13 5 = cos(180 − 4 5 ) = − cos 45 = − 2 ∘ ∘ ∘ ∘ tg 135 = tg (180 − 45 ) = − tg 45 = − 1 ctg 135 ∘ = ctg (180∘ − 45∘) = − ctg45∘ = − 1.$

Odpowiedź: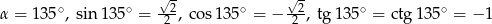
W zasadzie moglibyśmy postąpić podobnie jak w poprzednim podpunkcie rozbijając szukany kąt na dwa kąty, ale zamiast tego będziemy mądrzejsi i skorzystamy z ogólnej deﬁnicji funkcji trygonometrycznych.

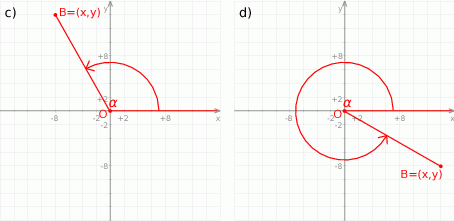
Wyliczmy na początek długość promienia wodzącego

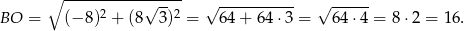
$∘ ----------------- 2 √ --2 √ ----------- √ ------ BO = (−8 ) + (8 3) = 64 + 64 ⋅3 = 64 ⋅4 = 8 ⋅2 = 1 6.$

Jeżeli oznaczymy 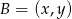to mamy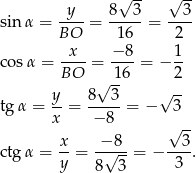

$√ -- √ -- sin α = -y--= 8--3-= --3- BO 16 2 -x-- −8-- 1- co sα = BO = 16 = − 2 √ -- √ -- tg α = y- = 8--3-= − 3 x − 8 √ -- x − 8 3 ctg α = -- = -√--- = − ----. y 8 3 3$

Łatwo odczytać z tych wartości, że .
Odpowiedź: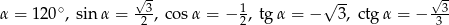
Wyliczmy na początek długość promienia wodzącego
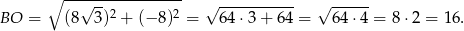
$∘ --√-------------- √ ----------- √ ------ BO = (8 3)2 + (− 8)2 = 64 ⋅3+ 64 = 64 ⋅4 = 8 ⋅2 = 1 6.$

Jeżeli oznaczymy 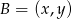to mamy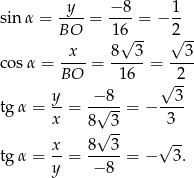

$sin α = --y- = −-8-= − 1- BO 16√ -- 2√ -- x 8 3 3 co sα = ----= -----= ---- BO 16 √ -2 y- -−-8- --3- tg α = x = 8 √ 3-= − 3 √ -- x- 8---3 √ -- tg α = y = − 8 = − 3.$

Łatwo odczytać z tych wartości, że 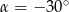lub jak ktoś woli .
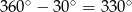Odpowiedź: