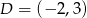Zadanie nr 1485427

Dane są współrzędne dwóch kolejnych wierzchołków kwadratu 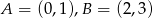ABCD : A = (0,1),B = (2,3) . Wyznacz współrzędne wierzchołka 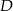, jeśli wiesz, że kwadrat jest zawarty w I i II ćwiartce układu współrzędnych.

Rozwiązanie

Zaczynamy od rysunku.

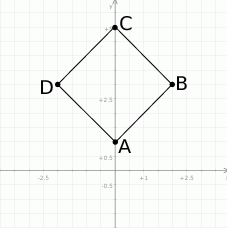
Sposób I

Łatwo możemy napisać równanie prostej 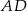: jest to prosta prostopadła do wektora −→ AB = [2,2] i przechodząca przez punkt 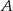. Ma zatem równanie

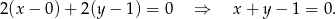
2(x − 0) + 2(y − 1) = 0 ⇒ x + y − 1 = 0.

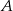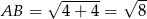Szukamy na tej prostej punktu, który jest odległy od o √ ------ √ -- AB = 4+ 4 = 8 . Punkt ten musi spełniać warunek

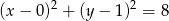
(x − 0 )2 + (y − 1)2 = 8

Podstawiamy w tej równości 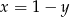x = 1 − y (z równania prostej).

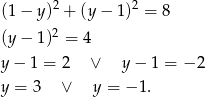
(1 − y)2 + (y− 1)2 = 8 (y − 1)2 = 4 y − 1 = 2 ∨ y− 1 = − 2 y = 3 ∨ y = − 1.

Ponieważ kwadrat ma być w I i II ćwiartce, daje to nam 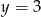y = 3 . Wtedy x = 1− y = − 2 .

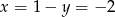Sposób II

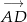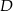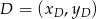Zadanie można też łatwo rozwiązać używając wektorów. Wektor −→ AD musi być prostopadły do − → AB = [2,2] i oba mają tę samą długość. Łatwo zatem zgadnąć (iloczyn skalarny ma być równy 0), że A−D→ = [− 2,2] lub A−D→ = [2,− 2] . Drugi z tych wektorów da nam punkt w IV ćwiartce, więc −→ AD = [−2 ,2] i możemy wyliczyć współrzędne punktu D = (x ,y ) D D .