/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 1601450

Dodaj do ulubionych
Dodaj do rozwiązanych

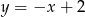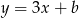Dane są proste o równaniach y = −x + 2 oraz y = 3x + b , które przecinają się w punkcie leżącym na osi 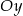Oy układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi Ox .

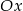Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

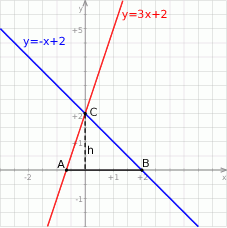
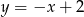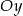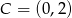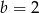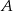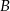Prosta y = −x + 2 przecina oś Oy w punkcie C = (0,2) , więc druga prosta też musi przechodzić przez ten punkt, czyli b = 2 . Wyznaczamy jeszcze punkty wspólne A i B danych prostych z osią Ox .

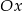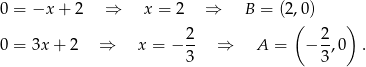
0 = −x + 2 ⇒ x = 2 ⇒ B = (2,0) ( ) 0 = 3x + 2 ⇒ x = − 2- ⇒ A = − 2,0 . 3 3

Pole trójkąta 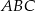ABC jest więc równe

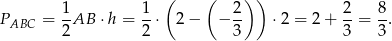
( ( ) ) P = 1AB ⋅h = 1⋅ 2 − − 2- ⋅ 2 = 2+ 2-= 8. ABC 2 2 3 3 3

 
Odpowiedź: 8 3

Wersja PDF