Zadanie nr 1611375
Boki 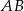 i
i 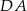 rombu
rombu 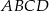 są zawarte odpowiednio w prostych o równaniach
są zawarte odpowiednio w prostych o równaniach 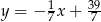 i
i 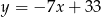 . Napisz równanie prostej zawierającej przekątną
. Napisz równanie prostej zawierającej przekątną 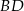 tego rombu, jeżeli jego środek ma współrzędne
tego rombu, jeżeli jego środek ma współrzędne 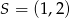 .
.
Rozwiązanie
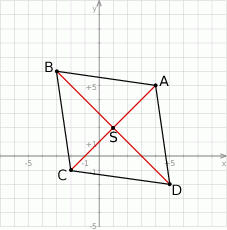
Szkicujemy romb z przekątnymi (nasz rysunek jest dość dokładny, ale do rozwiązania wystarczy zwykły schematyczny szkic rombu – nie musi być nawet w układzie współrzędnych).
Rozpoczynamy od wyznaczenia punktu 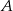 – jest to punkt wspólny dwóch podanych prostych.
– jest to punkt wspólny dwóch podanych prostych.
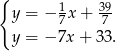
Porównujemy 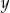 -ki i mamy
-ki i mamy
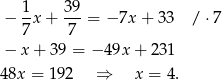
Stąd 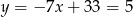 i
i 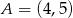 .
.
Sposób I
Ponieważ przekątne rombu są prostopadłe, równanie prostej 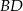 możemy łatwo napisać jako równanie prostej prostopadłej do
możemy łatwo napisać jako równanie prostej prostopadłej do 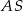 i przechodzącej przez
i przechodzącej przez 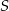 . Najpierw wyznaczamy więc równanie prostej
. Najpierw wyznaczamy więc równanie prostej 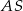 . Szukamy prostej w postaci
. Szukamy prostej w postaci 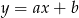 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 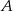 i
i 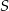 .
.
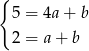
Odejmując równania stronami (żeby skrócić 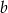 ) otrzymujemy
) otrzymujemy 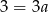 , czyli
, czyli 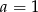 . Współczynnika
. Współczynnika 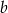 możemy nie wyznaczać, bo nie jest nam potrzebny. Prosta
możemy nie wyznaczać, bo nie jest nam potrzebny. Prosta 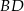 jest prostopadła do
jest prostopadła do 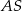 , więc ma równanie postaci
, więc ma równanie postaci 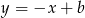 . Współczynnik
. Współczynnik 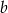 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 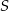 .
.

Interesująca nas przekątna 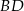 ma więc równanie
ma więc równanie 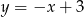 .
.
Sposób II
Tym razem wyznaczymy współrzędne pozostałych wierzchołków rombu. Zaczynamy od 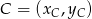 – punkt
– punkt 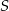 jest środkiem odcinka
jest środkiem odcinka 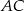 , więc
, więc
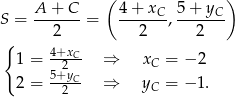
Zatem 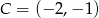 . Aby wyznaczyć współrzędne punktu
. Aby wyznaczyć współrzędne punktu 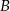 piszemy równanie prostej
piszemy równanie prostej 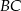 . Prosta ta jest równoległa do
. Prosta ta jest równoległa do 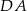 , więc ma równanie postaci
, więc ma równanie postaci 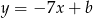 . Współczynnik
. Współczynnik 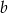 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 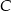 .
.
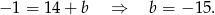
Prosta 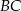 ma więc równanie
ma więc równanie 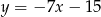 . Wyznaczamy teraz jej punkt wspólny
. Wyznaczamy teraz jej punkt wspólny 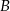 z prostą
z prostą 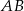 .
.
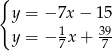
Porównujemy 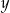 -ki i mamy
-ki i mamy
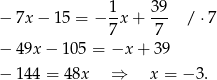
Stąd 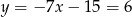 i
i 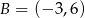 . Pozostało teraz napisać równanie prostej
. Pozostało teraz napisać równanie prostej 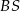 (czyli przekątnej
(czyli przekątnej 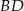 ). Szukamy prostej w postaci
). Szukamy prostej w postaci 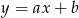 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 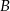 i
i 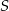 .
.
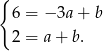
Odejmujemy od drugiego równania pierwsze i mamy 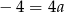 , czyli
, czyli 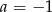 . Stąd
. Stąd 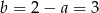 i interesująca nas przekątna ma równanie
i interesująca nas przekątna ma równanie 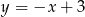 .
.
Sposób III
Korzystamy ze wzoru na równanie prostej prostopadłej do wektora ![→ v = [p ,q]](https://img.zadania.info/zad/1611375/HzadR58x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 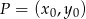
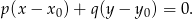
W naszej sytuacji mamy
![→v = −S→A = [4− 1,5− 2] = [3,3],](https://img.zadania.info/zad/1611375/HzadR61x.gif)
a punkt to 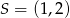 . Szukane równanie przekątnej ma więc postać.
. Szukane równanie przekątnej ma więc postać.
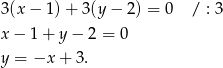
Odpowiedź: