/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 1644744

Dodaj do ulubionych
Dodaj do rozwiązanych

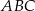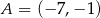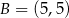Na rysunku przedstawione są dwa wierzchołki trójkąta prostokątnego ABC : A = (− 7,− 1) i B = (5,5) oraz prosta o równaniu 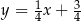y = 14 x+ 34 , zawierająca przeciwprostokątną 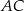AC tego trójkąta.

PIC

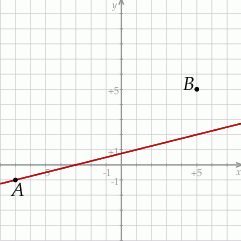
Oblicz współrzędne wierzchołka 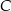C tego trójkąta i długość odcinka AC .

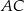Rozwiązanie

Dorysujmy szukany przez nas trójkąt prostokątny.

PIC

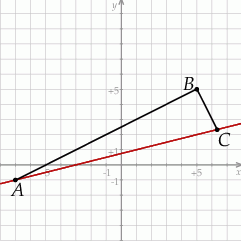
Sposób I

Napiszmy najpierw równanie prostej 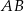AB . Szukamy prostej w postaci 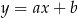y = ax + b i podstawiamy współrzędne punktów 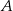A i B .

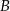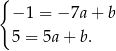
{ −1 = − 7a+ b 5 = 5a + b.

Odejmujemy od drugiego równania pierwsze i mamy

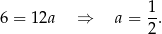
1 6 = 12a ⇒ a = --. 2

Współczynnika 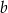b nie obliczamy, bo nie będzie nam potrzebny.

Napiszemy teraz równanie prostej 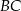BC jest to prosta prostopadła do 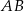AB , więc ma równanie postaci 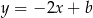y = −2x + b . Współczynnik 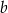b wyznaczamy podstawiając współrzędne punktu B .

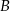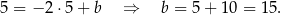
5 = − 2⋅ 5+ b ⇒ b = 5 + 10 = 1 5.

Zatem prosta 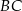BC ma równanie 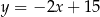y = − 2x + 15 . Wyznaczamy teraz jej punkt wspólny 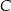C z podaną przeciwprostokątną AC .

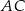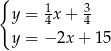
{ y = 14x + 34 y = − 2x + 15

Odejmujemy od pierwszego równania drugie i mamy

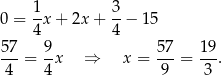
1 3 0 = --x+ 2x+ --− 15 4 4 57- 9- 57- 19- 4 = 4x ⇒ x = 9 = 3 .

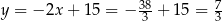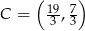Stąd y = − 2x + 1 5 = − 338+ 15 = 73 i ( ) C = 139, 73 .

Pozostało obliczyć długość odcinka 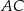AC .

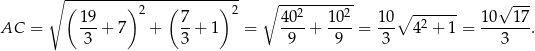
------------------------ ∘ ( )2 ( ) 2 ∘ ---2-----2- ∘ ------- √ --- AC = 19-+ 7 + 7-+ 1 = 40--+ 10--= 10- 42 + 1 = 1-0--17. 3 3 9 9 3 3

Sposób II

Tym razem współrzędne punktu 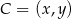C = (x ,y ) wyznaczymy pisząc twierdzenie Pitagorasa w trójkącie ABC .

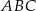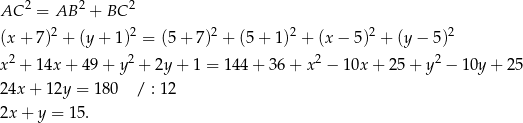
2 2 2 AC = AB + BC (x + 7)2 + (y+ 1)2 = (5 + 7)2 + (5+ 1)2 + (x− 5)2 + (y− 5)2 2 2 2 2 x + 14x + 49 + y + 2y + 1 = 144 + 36 + x − 10x + 2 5+ y − 1 0y+ 25 24x + 12y = 180 / : 12 2x + y = 1 5.

Zauważmy teraz, że punkt 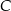C leży na podanej prostej 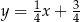y = 1x+ 3 4 4 , więc mamy

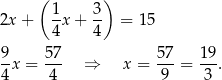
( ) 1 3 2x + -x + -- = 15 4 4 9- 57- 57- 19- 4x = 4 ⇒ x = 9 = 3 .

Stąd

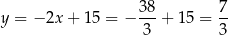
y = − 2x+ 15 = − 38-+ 15 = 7- 3 3

i 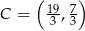( ) C = 193 , 73 . Długość odcinka 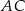AC obliczmy tak samo jak w poprzednim sposobie.  
Odpowiedź: 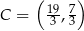( 19 7) C = 3 , 3 i 10√ 17- |AC | = --3--

Wersja PDF