Zadanie nr 1744349
Środek okręgu, stycznego do osi 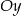 i do prostej o równaniu
i do prostej o równaniu 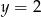 , ma obie współrzędne ujemne. Promień okręgu ma długość 5. Wyznacz równanie tego okręgu.
, ma obie współrzędne ujemne. Promień okręgu ma długość 5. Wyznacz równanie tego okręgu.
Rozwiązanie
Szkicujemy opisany okrąg.
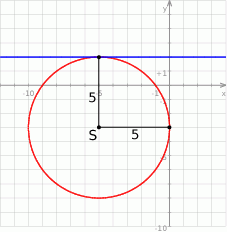
Szukany okrąg jest styczny do osi 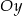 i promień okręgu wynosi 5, więc pierwsza współrzędna środka
i promień okręgu wynosi 5, więc pierwsza współrzędna środka 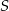 okręgu musi być równa
okręgu musi być równa 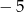 (bo mus być ujemna). Ponadto okrąg jest styczny do prostej
(bo mus być ujemna). Ponadto okrąg jest styczny do prostej 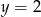 , więc druga współrzędna środka
, więc druga współrzędna środka 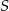 musi być równa
musi być równa 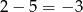 . Zatem
. Zatem 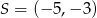 . Teraz już łatwo zapisać równanie okręgu
. Teraz już łatwo zapisać równanie okręgu
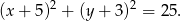
Odpowiedź: