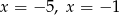/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 1868025

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz równania stycznych do okręgu 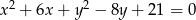2 2 x + 6x + y − 8y + 21 = 0 równoległych do osi Oy .

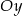Rozwiązanie

Na początku przekształćmy dane równanie okręgu tak, aby wiedzieć jaki jest jego środek i promień (zwijamy do pełnych kwadratów).

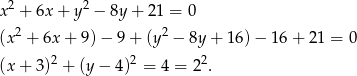
2 2 x + 6x+ y − 8y+ 21 = 0 (x2 + 6x+ 9)− 9+ (y2 − 8y+ 16)− 16+ 21 = 0 (x+ 3)2 + (y − 4 )2 = 4 = 22.

Jest to więc okrąg o środku 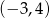(− 3,4) i promieniu r = 2 .

PIC

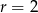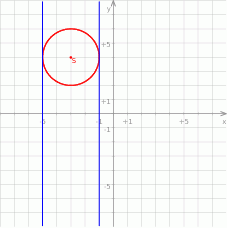
Z obrazka widać teraz, że styczne równoległe do osi 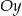Oy to pionowe proste, których odległość od środka okręgu jest równa 2. Są dwie takie proste: 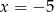x = −5 i x = − 1 .  
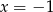Odpowiedź: x = −5 , x = −1

Wersja PDF