Zadanie nr 1919544
Dane są punkty 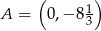 i
i 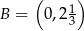 . Wyznacz na prostej
. Wyznacz na prostej 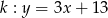 punkt
punkt 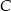 , tak aby
, tak aby 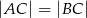 . Dla wyznaczonego punktu C:
. Dla wyznaczonego punktu C:
- wykaż, że trójkąt
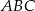 jest prostokątny;
jest prostokątny; - wyznacz równanie okręgu opisanego na trójkącie
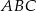 .
.
Rozwiązanie
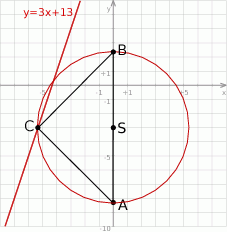
Możemy rozpocząć od szkicowego rysunku.
-
Sposób I
Równość
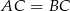 oznacza, że punkt
oznacza, że punkt 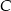 leży na symetralnej odcinka
leży na symetralnej odcinka 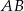 . Ponieważ punkty te leżą na osi
. Ponieważ punkty te leżą na osi 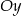 łatwo napisać równanie tej symetralnej – jest to pozioma prosta przechodząca przez środek
łatwo napisać równanie tej symetralnej – jest to pozioma prosta przechodząca przez środek 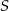 odcinka
odcinka 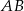 , czyli prosta
, czyli prosta 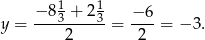
Szukamy teraz punktu wspólnego tej prostej z daną prostą.
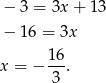
Zatem
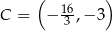 .
. Ponieważ trójkąt
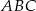 jest równoramienny (
jest równoramienny (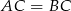 ), jego przeciwprostokątną musi być odcinek
), jego przeciwprostokątną musi być odcinek 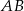 . Sprawdźmy, czy rzeczywiście
. Sprawdźmy, czy rzeczywiście 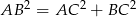 .
. 
Sposób II
Szukamy punktu
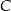 w postaci
w postaci 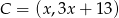 .
. 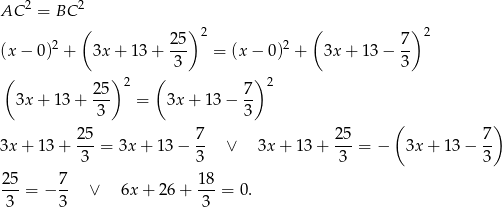
Pierwsze równanie jest sprzeczne, a z drugiego mamy
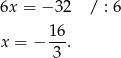
Stąd
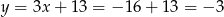 i
i 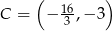 . Równość
. Równość 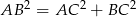 uzasadniamy jak w poprzednim sposobie.
uzasadniamy jak w poprzednim sposobie.
Odpowiedź: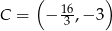
- Środkiem okręgu opisanego na trójkącie prostokątnym jest środek jego przeciwprostokątnej, czyli punkt
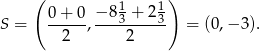
Jego promień to odległość środka od jednego z wierzchołków, np.
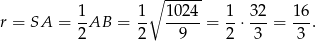
Okrąg opisany na trójkącie
 ma więc równanie:
ma więc równanie: 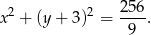
Odpowiedź: