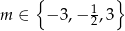Zadanie nr 1939500
Dane są punkty 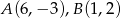 oraz
oraz 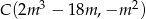 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 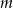 , dla których proste
, dla których proste 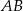 i
i 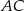 są prostopadłe.
są prostopadłe.
Rozwiązanie
Sposób I
Współczynnik kierunkowy prostej 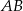 jest równy
jest równy
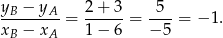
Zatem współczynnik kierunkowy prostej 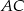 musi być równy 1. Mamy stąd równanie
musi być równy 1. Mamy stąd równanie
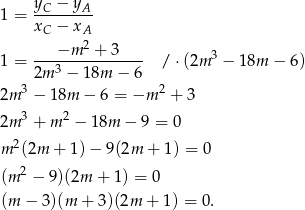
Zatem 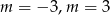 lub
lub 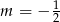 .
.
Sposób II
Sprawdzamy, kiedy wektory 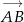 i
i 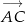 są prostopadłe.
są prostopadłe.
![−→ −→ AB ∘AC = 0 [1− 6,2+ 3]∘ [2m 3 − 18m − 6,−m 2 + 3] = 0 3 2 [−5 ,5]∘ [2m − 18m − 6,−m + 3] = 0 − 5(2m 3 − 18m − 6 )+ 5 (−m 2 + 3) = 0 / : (− 5) 3 2 2m − 18m − 6+ m − 3 = 0 2m 3 + m2 − 18m − 9 = 0 m 2(2m + 1 )− 9(2m + 1) = 0 2 (m − 9 )(2m + 1) = 0 (m − 3 )(m + 3)(2m + 1) = 0 .](https://img.zadania.info/zad/1939500/HzadR8x.gif)
Zatem 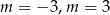 lub
lub 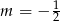 .
.
Sposób III
Jeżeli proste 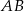 i
i 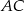 mają być prostopadłe, to trójkąt
mają być prostopadłe, to trójkąt 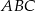 musi być prostokątny i
musi być prostokątny i 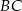 musi być jego przeciwprostokątną. Mamy zatem równanie
musi być jego przeciwprostokątną. Mamy zatem równanie
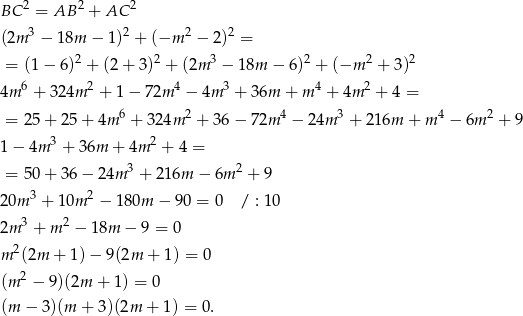
Zatem 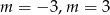 lub
lub 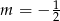 .
.
Odpowiedź: