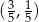Zadanie nr 2004756
Na prostej 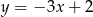 wyznacz punkt, którego suma kwadratów odległości od osi układu współrzędnych jest najmniejsza.
wyznacz punkt, którego suma kwadratów odległości od osi układu współrzędnych jest najmniejsza.
Rozwiązanie
Szukamy punktu postaci 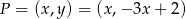 . Odległość tego punktu od osi
. Odległość tego punktu od osi 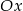 to
to 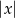 , a odległość od osi
, a odległość od osi 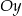 to
to 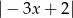 . Zatem suma kwadratów tych liczb to
. Zatem suma kwadratów tych liczb to
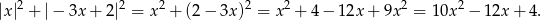
Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w górę, więc jej najmniejszą wartość otrzymamy w wierzchołku, czyli dla
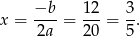
Wtedy
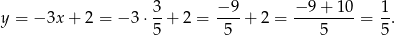
Odpowiedź: