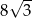/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 2037379

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest okrąg 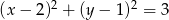2 2 (x− 2) + (y − 1 ) = 3 . Oblicz pole rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę 60∘ .

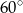Rozwiązanie

Jedyna informacja dotycząca podanego okręgu, która jest istotna to jego promień 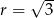√ -- r = 3 . Położenie tego okręgu w układzie współrzędnych nie ma żadnego znaczenia.

Wykonajmy rysunek.

PIC

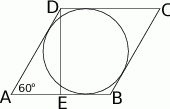
Średnica okręgu wpisanego w romb to dokładnie wysokość tego rombu, zatem 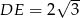√ -- DE = 2 3 . Z trójkąta prostokątnego 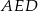AED mamy więc

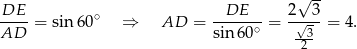
√ -- DE-- ∘ -DE---- 2--3- AD = sin 60 ⇒ AD = sin 60∘ = √-3 = 4. 2

Możemy więc obliczyć pole rombu

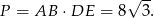
√ -- P = AB ⋅DE = 8 3.

 
Odpowiedź: √ -- 8 3

Wersja PDF