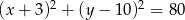Zadanie nr 2128749
Napisz równanie okręgu, do którego należą punkty wspólne paraboli 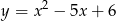 i prostej
i prostej 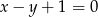 , a którego środek należy do prostej o równaniu
, a którego środek należy do prostej o równaniu 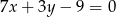 .
.
Rozwiązanie
Rozpocznijmy od wyznaczenia punktów wspólnych podanych: paraboli i prostej. Podstawiamy 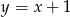 do równania paraboli.
do równania paraboli.
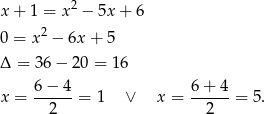
Stąd odpowiednio 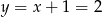 i
i 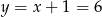 , czyli punkty wspólne to
, czyli punkty wspólne to 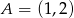 i
i 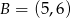 . Teraz pora na szkicowy rysunek.
. Teraz pora na szkicowy rysunek.
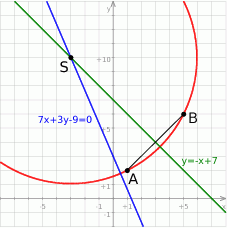
Wiemy, że środek szukanego okręgu leży na prostej 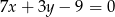 . Leży on też na symetralnej odcinka
. Leży on też na symetralnej odcinka 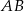 . Napiszmy równanie tej symetralnej. Można to zrobić na różne sposoby, my zrobimy to myśląc o symetralnej jak o zbiorze punktów, które są równo odległe od punktów
. Napiszmy równanie tej symetralnej. Można to zrobić na różne sposoby, my zrobimy to myśląc o symetralnej jak o zbiorze punktów, które są równo odległe od punktów  i
i  , czyli symetralna jest zbiorem punktów
, czyli symetralna jest zbiorem punktów  opisanych równaniem
opisanych równaniem
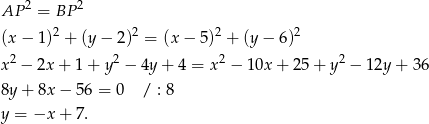
Szukamy teraz punktu wspólnego tej symetralnej z podaną prostą – podstawiamy 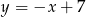 do równania tej prostej.
do równania tej prostej.
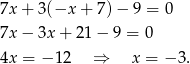
Stąd 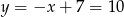 i
i 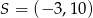 .
.
Liczymy jeszcze długość promienia okręgu
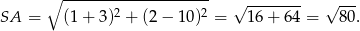
Szukany okrąg ma więc równanie
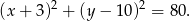
Odpowiedź: