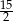/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 2153678

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz pole i obwód trójkąta o wierzchołkach: 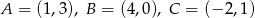A = (1,3), B = (4,0), C = (− 2,1) .

Rozwiązanie

Na początek możemy sobie naszkicować podane punkty.

PIC

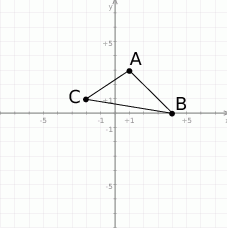
Najpierw policzmy obwód. W tym celu liczymy długości boków trójkąta.

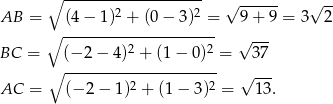
∘ ------------------- √ ------ √ -- AB = (4 − 1)2 + (0− 3)2 = 9 + 9 = 3 2 ∘ --------------------- 2 2 √ --- BC = ∘ (−-2−--4)-+--(1−-0-)-= 37 2 2 √ --- AC = (− 2 − 1) + (1− 3) = 13.

Zatem obwód jest równy.

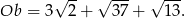
√ -- √ --- √ --- Ob = 3 2+ 37+ 13.

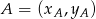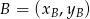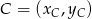Aby wyliczyć pole trójkąta, korzystamy ze wzoru na pole trójkąta o wierzchołkach A = (xA,yA ) , B = (xB,yB ) i C = (xC ,yC) .

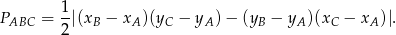
1- PABC = 2 |(xB − xA)(yC − yA) − (yB − yA )(xC − xA )|.

W naszej sytuacji mamy

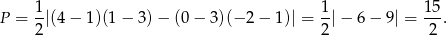
P = 1-|(4 − 1)(1 − 3) − (0 − 3)(− 2 − 1)| = 1-|− 6 − 9| = 1-5. 2 2 2

 
Odpowiedź: Obwód: 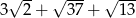√ -- √ --- √ --- 3 2 + 37 + 13 , pole: 152

Wersja PDF