/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 2195713

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest okrąg 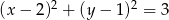2 2 (x− 2) + (y− 1) = 3 . Oblicz długości przekątnych rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę 60∘ .

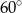Rozwiązanie

Jedyna informacja dotycząca podanego okręgu, która jest istotna, to jego promień 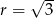√ -- r = 3 . Położenie tego okręgu w układzie współrzędnych nie ma żadnego znaczenia.

Wykonajmy rysunek.

PIC

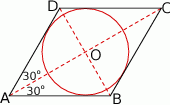
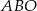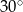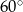Ponieważ przekątne rombu są dwusiecznymi jego kątów wewnętrznych, są prostopadłe i dzielą się na połowy, więc trójkąt ABO jest prostokątny i jego kąty ostre to 30 ∘ i 60∘ . Mamy zatem

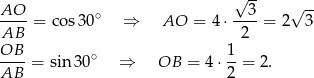
√ -- AO ∘ 3 √ -- ----= cos30 ⇒ AO = 4⋅ ----= 2 3 AB 2 OB--= sin 30∘ ⇒ OB = 4⋅ 1-= 2. AB 2

Przekątne mają więc długości 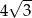√ -- 4 3 i 4 .  
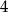Odpowiedź: 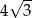√ -- 4 3 i 4

Wersja PDF