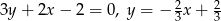/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 2210775

Dodaj do ulubionych
Dodaj do rozwiązanych

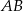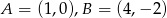Zapisz równanie ogólne i kierunkowe prostej AB , jeśli A = (1,0),B = (4 ,− 2 ) .

Rozwiązanie

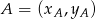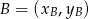Równanie prostej przechodzącej przez dwa punkty A = (xA ,yA) i B = (xB,yB ) to

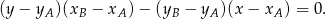
(y− yA)(xB − xA ) − (yB − yA )(x− xA) = 0.

Wstawiamy do powyższego wzoru.

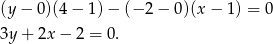
(y − 0)(4 − 1) − (− 2 − 0)(x − 1) = 0 3y + 2x − 2 = 0.

Otrzymana postać to postać ogólna. Aby wyznaczyć postać kierunkową musimy wyliczyć 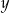y .

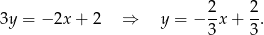
2 2 3y = − 2x + 2 ⇒ y = − --x+ -. 3 3

 
Odpowiedź: 2 2 3y + 2x − 2 = 0, y = − 3x + 3

Wersja PDF