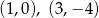Zadanie nr 2424234
Punkty 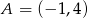 oraz
oraz 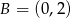 należą do prostej
należą do prostej 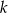 . Punkt
. Punkt 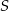 ma współrzędne
ma współrzędne 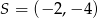 . Oblicz współrzędne punktów należących do prostej
. Oblicz współrzędne punktów należących do prostej 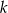 , których odległość od punktu
, których odległość od punktu 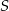 wynosi 5.
wynosi 5.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
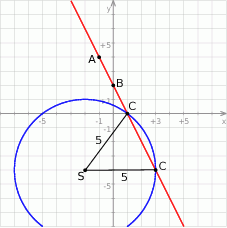
Wyznaczymy najpierw równanie prostej 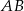 . Szukamy prostej w postaci
. Szukamy prostej w postaci 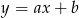 . Podstawiamy współrzędne punktów
. Podstawiamy współrzędne punktów 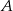 i
i 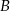 .
.
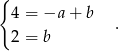
Zatem

i prosta  ma równanie
ma równanie 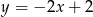 .
.
Szukamy teraz punktu 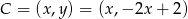 na tej prostej, którego odległość od punktu
na tej prostej, którego odległość od punktu 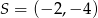 jest równa 5.
jest równa 5.
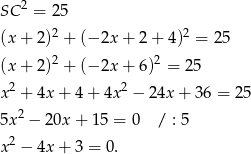
Obliczamy wyróżnik i pierwiastki
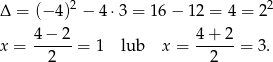
Wtedy odpowiednio
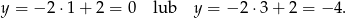
Mamy zatem 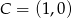 lub
lub 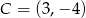 .
.
Odpowiedź: