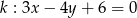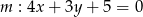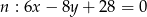Zadanie nr 2773519
Figura 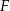 jest sumą dwóch prostych o równaniach
jest sumą dwóch prostych o równaniach 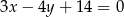 oraz
oraz 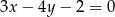 . Sprawdź czy podana prosta jest osią symetrii tej figury:
. Sprawdź czy podana prosta jest osią symetrii tej figury:
Rozwiązanie
Podane proste są równoległe (mają ten sam współczynnik kierunkowy  ), więc osią symetrii figury
), więc osią symetrii figury 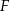 jest dowolna prosta prostopadła do podanych prostych oraz prosta, która jest dokładnie pośrodku pomiędzy danymi prostymi. Równanie tej ostatniej prostej można łatwo odgadnąć:
jest dowolna prosta prostopadła do podanych prostych oraz prosta, która jest dokładnie pośrodku pomiędzy danymi prostymi. Równanie tej ostatniej prostej można łatwo odgadnąć:
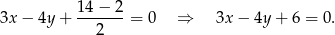
Jeżeli nie chcemy zgadywać, to zapisujemy równania w postaci 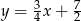 i
i 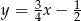 . Proste te przecinają oś
. Proste te przecinają oś 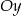 na poziomach
na poziomach 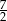 i
i 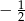 , więc interesująca nas prosta musi przecinać oś na poziomie
, więc interesująca nas prosta musi przecinać oś na poziomie 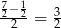 . Zatem prosta ta ma równanie
. Zatem prosta ta ma równanie
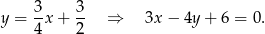
- Podana prosta to dokładnie znaleziona przez nas prosta równo odległa od podanych prostych.
Odpowiedź: Tak, jest. - Podana prosta jest prostopadła do podanych prostych (ma współczynnik kierunkowy
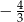 ), więc jest osią symetrii.
), więc jest osią symetrii.
Odpowiedź: Tak, jest. - Jeżeli podzielimy równanie przez 2, to mamy
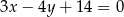 . Jest to pierwsza z danych prostych, więc nie jest osią symetrii figury
. Jest to pierwsza z danych prostych, więc nie jest osią symetrii figury 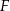 .
.
Odpowiedź: Nie, nie jest. - Prosta ta ani nie jest równoległa, ani prostopadła do danych prostych. Nie może więc być ich osią symetrii.
Odpowiedź: Nie, nie jest.
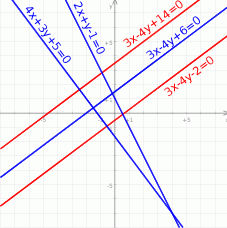
Na koniec obrazek całej sytuacji.