/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 2836866

Dodaj do ulubionych
Dodaj do rozwiązanych

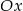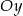Rozpatrujemy wszystkie prostokąty o polu równym 6, których dwa sąsiednie boki zawarte są w osiach Ox i Oy układu współrzędnych. Wyznacz równanie krzywej będącej zbiorem tych wierzchołków rozpatrywanych prostokątów, które nie leżą na żadnej z osi układu współrzędnych. Narysuj tę krzywą.

Rozwiązanie

Jeżeli zaczniemy sobie szkicować możliwe położenia opisanych prostokątów, to widać, że jego wierzchołki muszą mieć współrzędne postaci 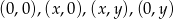(0,0),(x ,0),(x,y),(0,y) .

PIC

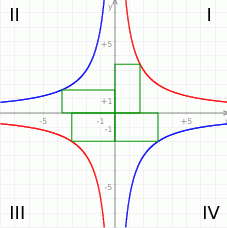
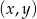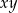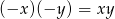Ponieważ punkt (x,y) może leżeć w jednej z 4 ćwiartek układu współrzędnych, mamy 4 różne przypadki. Jeżeli leży on w I lub III ćwiartce, to pole prostokąta jest odpowiednio równe xy lub (−x )(−y ) = xy . Mamy więc w tej sytuacji równanie

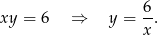
6 xy = 6 ⇒ y = -. x

Wykresem tej funkcji jest hiperbola, której gałęzie leżą w I i III ćwiartce układu współrzędnych.

Jeżeli natomiast punkt 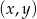(x,y) leży w II lub IV ćwiartce układu współrzędnych, to pole jest równe 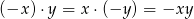(−x )⋅y = x⋅ (−y ) = −xy i mamy równanie

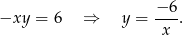
−xy = 6 ⇒ y = −-6. x

Wykres tej funkcji powstaje z wykresu funkcji 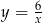y = 6x przez odbicie względem osi Ox .  
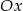Odpowiedź: y = ± 6 x

Wersja PDF