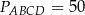Zadanie nr 2974004
Dany jest kwadrat 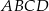 , w którym
, w którym 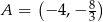 . Przekątna
. Przekątna 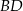 tego kwadratu jest zawarta w prostej o równaniu
tego kwadratu jest zawarta w prostej o równaniu 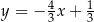 . Oblicz współrzędne punktu przecięcia przekątnych
. Oblicz współrzędne punktu przecięcia przekątnych 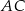 i
i 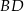 oraz pole kwadratu
oraz pole kwadratu 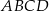 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku
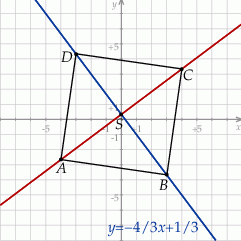
Przekątna 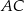 jest zawarta w prostej prostopadłej do prostej
jest zawarta w prostej prostopadłej do prostej 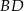 , więc ma równanie postaci
, więc ma równanie postaci 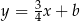 . Ponadto przechodzi przez punkt
. Ponadto przechodzi przez punkt 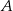 , więc
, więc
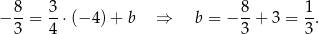
Prosta  ma więc równanie
ma więc równanie 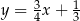 . Szukamy teraz jest punktu wspólnego
. Szukamy teraz jest punktu wspólnego 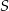 z przekątną
z przekątną 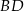 .
.
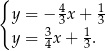
Odejmujemy od drugiego równania pierwsze i mamy
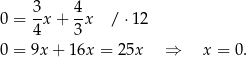
Stąd 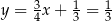 i
i 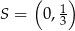 .
.
Jeżeli oznaczymy przez  długość boku kwadratu, to mamy
długość boku kwadratu, to mamy
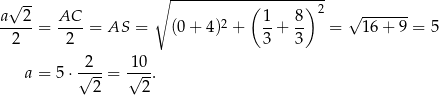
Pole kwadratu  jest więc równe
jest więc równe
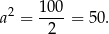
Odpowiedź: 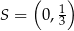 ,
,