Zadanie nr 3061409
Dana jest prosta 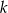 o równaniu parametrycznym
o równaniu parametrycznym 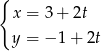 dla
dla 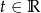 . Znajdź równanie parametryczne:
. Znajdź równanie parametryczne:
- prostej
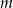 równoległej do prostej
równoległej do prostej 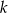 , przechodzącej przez punkt
, przechodzącej przez punkt 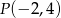 .
. - prostej
 prostopadłej do prostej
prostopadłej do prostej  , przechodzącej przez punkt
, przechodzącej przez punkt 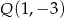 .
.
Rozwiązanie
Dana prosta jest równoległa do wektora ![[2,2]](https://img.zadania.info/zad/3061409/HzadR0x.gif) (współczynniki przy
(współczynniki przy 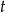 ).
).
- Szukana prosta ma być równoległa do tego samego wektora co
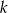 i przechodzić przez punkt
i przechodzić przez punkt 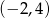 , więc jej równanie parametryczne to
, więc jej równanie parametryczne to 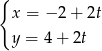 dla
dla 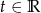 .
.
Odpowiedź: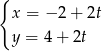 dla
dla 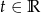
- Musimy zgadnąć wektor prostopadły do
![[2 ,2]](https://img.zadania.info/zad/3061409/HzadR8x.gif) . Nie jest to trudne, wystarczy wziąć np.
. Nie jest to trudne, wystarczy wziąć np. ![[1,− 1]](https://img.zadania.info/zad/3061409/HzadR9x.gif) (iloczyn skalarny ma być 0). Zatem szukane równanie to
(iloczyn skalarny ma być 0). Zatem szukane równanie to 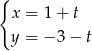 dla
dla 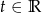 .
.
Odpowiedź: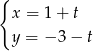 dla
dla 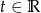
Na koniec obrazek.