Zadanie nr 3174011
Jeden z boków kwadratu 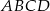 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 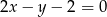 . Wierzchołek
. Wierzchołek 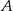 ma współrzędne
ma współrzędne 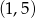 .
.
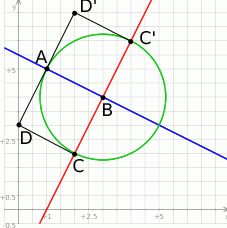
- Znajdź współrzędne pozostałych wierzchołków.
- Oblicz pole kwadratu
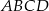 .
.
Rozwiązanie
Aby wyznaczyć wierzchołek 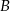 , napiszmy równanie prostej prostopadłej do danej prostej
, napiszmy równanie prostej prostopadłej do danej prostej 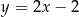 i przechodzącej przez punkt
i przechodzącej przez punkt 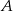 .
.
Prosta ta jest postaci 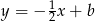 oraz przechodzi przez
oraz przechodzi przez 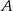 , więc
, więc
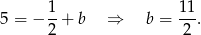
Znajdujemy punkt wspólny 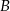 obu prostych
obu prostych
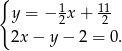
Dodajemy równania stronami (żeby skrócić 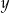 )
)
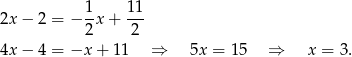
Stąd 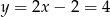 i
i 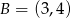 . Długość boku kwadratu wynosi
. Długość boku kwadratu wynosi
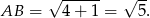
Aby znaleźć kolejny wierzchołek szukamy na prostej 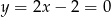 punktów
punktów 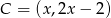 odległych od
odległych od 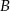 o
o 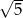 .
.
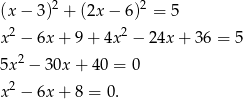
Dalej 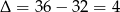 ,
, 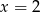 lub
lub 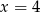 . Wtedy odpowiednio
. Wtedy odpowiednio 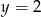 lub
lub 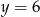 . Mamy więc dwie możliwości:
. Mamy więc dwie możliwości: 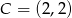 lub
lub 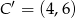 . Czwarty wierzchołek
. Czwarty wierzchołek 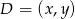 najłatwiej wyznaczyć posługując się wektorami.
najłatwiej wyznaczyć posługując się wektorami.
![→ → → → ′ ′ AD = BC AD = BC [x − 1,y − 5] = [− 1,− 2] [x− 1,y− 5] = [1,2] (x ,y) = (0,3) (x,y) = (2,7).](https://img.zadania.info/zad/3174011/HzadR27x.gif)
W obu przypadkach pole jest równe 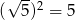 .
.
Odpowiedź: Wierzchołki 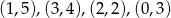 lub
lub 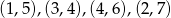 , pole: 5
, pole: 5

