Zadanie nr 3303604
Oblicz współrzędne środka 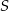 i skalę
i skalę 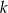 jednokładności, w której obrazem odcinka
jednokładności, w której obrazem odcinka 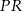 jest odcinek
jest odcinek 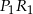 i wiadomo, że
i wiadomo, że 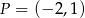 ,
, 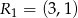 ,
, ![−→ SP 1 = [3,9]](https://img.zadania.info/zad/3303604/HzadT6x.gif) i
i ![−→ SR = [2 ,1]](https://img.zadania.info/zad/3303604/HzadT7x.gif) .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
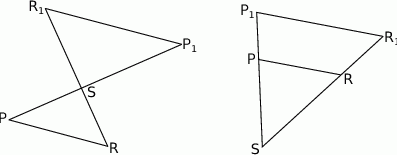
Sposób I
Na początku nie bardzo widać o co się w tym zadaniu zaczepić, więc spróbujmy po prostu zapisać, że punkty 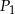 i
i 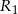 są obrazami
są obrazami 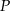 i
i 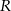 w jednokładności o środku
w jednokładności o środku 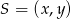 i skali
i skali 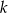 . Zwróćmy uwagę, że poniższe równania są prawdziwe niezależnie od tego, czy skala jednokładności jest dodatnia (prawy obrazek), czy ujemna (lewy obrazek)
. Zwróćmy uwagę, że poniższe równania są prawdziwe niezależnie od tego, czy skala jednokładności jest dodatnia (prawy obrazek), czy ujemna (lewy obrazek)
![( −→ −→ { SP 1 = k ⋅SP ( −→ −→ SR 1 = k⋅SR . { [3,9] = k ⋅[−2 − x ,1− y] [3 − x,1 − y] = k ⋅[2,1]. ( | 3 = −k (x+ 2) ||{ 9 = k(1− y) || 3 − x = 2k |( 1 − y = k](https://img.zadania.info/zad/3303604/HzadR7x.gif)
Podstawiając 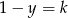 z czwartego równania do drugiego mamy
z czwartego równania do drugiego mamy
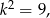
czyli 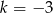 lub
lub 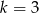 . Wtedy z pierwszego równania mamy odpowiednio
. Wtedy z pierwszego równania mamy odpowiednio 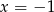 i
i 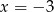 . Łatwo sprawdzić, że tylko rozwiązanie
. Łatwo sprawdzić, że tylko rozwiązanie 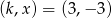 spełnia trzecie równanie. Zatem
spełnia trzecie równanie. Zatem 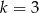 i czwartego równania mamy
i czwartego równania mamy 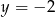 . Stąd
. Stąd 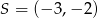 . Na koniec dokładniejszy rysunek w układzie współrzędnych.
. Na koniec dokładniejszy rysunek w układzie współrzędnych.
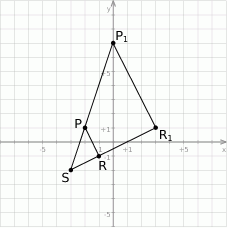
Sposób II
Gdy popatrzymy na schematyczny rysunek opisanej sytuacji, to widać, że podane informacje pozwalają napisać równania prostych 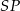 i
i 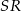 – pierwsza z nich to prosta przechodząca przez
– pierwsza z nich to prosta przechodząca przez  i równoległa do wektora
i równoległa do wektora 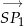 , a druga to prosta przechodząca przez
, a druga to prosta przechodząca przez 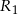 i równoległa do wektora
i równoległa do wektora 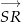 . Parametryczne równania tych prostych to odpowiednio
. Parametryczne równania tych prostych to odpowiednio
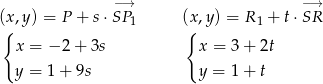
Szukamy punktu wspólnego tych prostych (czyli punktu 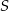 ) porównując odpowiednie współrzędne.
) porównując odpowiednie współrzędne.
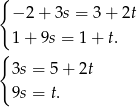
Podstawiamy teraz 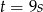 z drugiego równania do pierwszego i mamy
z drugiego równania do pierwszego i mamy
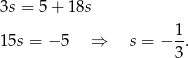
Teraz z równania prostej 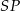 obliczamy współrzędne punktu
obliczamy współrzędne punktu 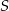
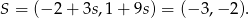
Mamy w takim razie
![−→ −→ SR 1 = [3 + 3,1 + 2] = [6,3] = 3 ⋅[2,1] = SR ,](https://img.zadania.info/zad/3303604/HzadR33x.gif)
co oznacza, że skala jednokładności jest równa 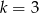 .
.
Odpowiedź: 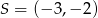 i
i 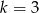 A) B) C) D)
A) B) C) D)

