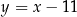Zadanie nr 3333021
Okrąg  o równaniu
o równaniu 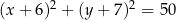 oraz okrąg
oraz okrąg 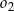 o środku
o środku 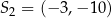 są wewnętrznie styczne, przy czym okrąg
są wewnętrznie styczne, przy czym okrąg 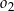 zawiera się w kole opisanym nierównością
zawiera się w kole opisanym nierównością 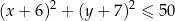 . Napisz równanie wspólnej stycznej do obu okręgów.
. Napisz równanie wspólnej stycznej do obu okręgów.
Rozwiązanie
Okrąg 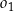 to okrąg o środku
to okrąg o środku 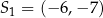 i promieniu
i promieniu 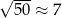 . Okrąg
. Okrąg 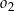 ma środek
ma środek 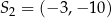 , zawiera się w kole
, zawiera się w kole  oraz jest styczny wewnętrznie do
oraz jest styczny wewnętrznie do 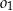 . Szkicujemy tę sytuację.
. Szkicujemy tę sytuację.
Zauważmy najpierw, że punkt styczności  okręgów
okręgów 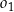 i
i 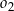 leży na prostej
leży na prostej 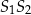 łączącej ich środki. Napiszmy równanie tej prostej. Szukamy prostej w postaci
łączącej ich środki. Napiszmy równanie tej prostej. Szukamy prostej w postaci 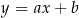 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 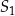 i
i 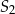 .
.
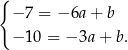
Odejmujemy od drugiego równania pierwsze (żeby skrócić 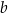 ) i mamy
) i mamy
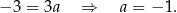
Stąd 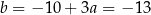 prosta
prosta 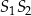 ma równanie
ma równanie 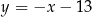 . Szukamy teraz punktu wspólnego
. Szukamy teraz punktu wspólnego 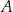 tej prostej oraz okręgu
tej prostej oraz okręgu 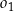 – podstawiamy
– podstawiamy 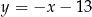 do równania okręgu.
do równania okręgu.
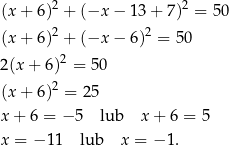
Pierwsze rozwiązanie oznaczałoby, że okrąg 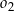 ma większy promień niż okrąg
ma większy promień niż okrąg 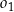 , co byłoby sprzeczne z założeniem, że
, co byłoby sprzeczne z założeniem, że 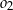 zawiera się w
zawiera się w 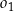 . Zatem
. Zatem 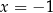 ,
, 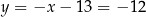 i
i 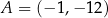 .
.
Pozostało napisać równanie wspólnej stycznej do okręgów 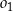 i
i 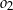 . Jest ona prostopadła do
. Jest ona prostopadła do 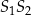 i przechodzi przez punkt
i przechodzi przez punkt 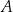 . Szukamy zatem prostej w postaci
. Szukamy zatem prostej w postaci 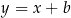 . Współczynnik
. Współczynnik 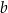 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 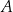 .
.

Interesująca nas styczna ma więc równanie 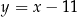 .
.
Odpowiedź: