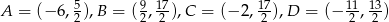/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 3335440

Dodaj do ulubionych
Dodaj do rozwiązanych

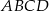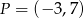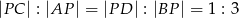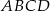W czworokącie ABCD przekątne przecinają się w punkcie o współrzędnych P = (− 3,7) w taki sposób, że |P C| : |AP | = |PD | : |BP | = 1 : 3 . Wiedząc, że − → AC = [4,6] i −→ BD = [− 10,− 2] , oblicz współrzędne wierzchołków tego czworokąta. Uzasadnij, że czworokąt ABCD jest trapezem.

Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

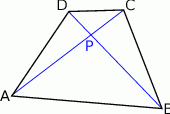
Z podanych informacji wiemy, że

−→ −→ [ ] AP = 3-AC = 3-[4 ,6] = 3, 9 . 4 4 2 [ 9] [− 3 − xA ,7− yA] = 3 ,-- { 2 − 3− x = 3 ⇒ x = −6 A 9 A 5 7− yA = 2 ⇒ yA = 2.

Zatem A = (− 6, 52) .

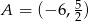Podobnie obliczamy współrzędne pozostałych wierzchołków czworokąta.

[ ] −→ 5- [4,6] = AC = xC + 6,yC − 2 { 4 = xC + 6 ⇒ xC = − 2 5 17 6 = yC − 2 ⇒ yC = 2 .

Zatem 17 C = (− 2,2-) .

−→ 3−→ 3 [ 1 5 3] BP = -BD = -[− 10,− 2] = − ---,− -- . 4 4 [ ] 2 2 15- 3- [− 3− xB,7 − yB ] = − 2 ,− 2 { −3 − xB = − 152 ⇒ xB = 92 3 17 7− yB = − 2 ⇒ yB = 2 .

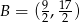Zatem 9 17 B = (2,-2 ) i pozostało obliczyć wierzchołek D .

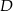−→ [ ] [−1 0,− 2] = BD = xD − 9-,yD − 17- 2 2 { 9 11- − 10 = xD − 2 ⇒ xD = − 2 − 2 = yD − 172 ⇒ yD = 132 .

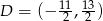Zatem D = (− 11, 13) 2 2 .

Fakt, że czworokąt 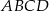ABCD jest trapezem uzasadnimy na dwa sposoby.

Sposób I

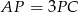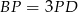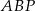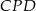Z treści zadania wiemy, że AP = 3PC i BP = 3P D . To oznacza, że trójkąty ABP i CP D są podobne w skali 3:1 (bo mają wspólny kąt przy wierzchołku 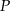P ). Zatem

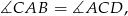
∡CAB = ∡ACD ,

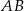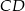co oznacza, że proste AB i CD są równoległe.

Sposób II

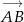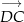Wystarczy wykazać, że wektory −→ AB i −→ DC są równoległe. Liczymy

−→ [ 11 1 7 13 ] [7 ] DC = − 2+ --,---− --- = --,2 [ 2 2 ] 2 [ 2] −→ 9 17 5 21 AB = --+ 6,---− -- = ---,6 . 2 2 2 2

Widać stąd, że 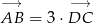−→ −→ AB = 3⋅DC , co kończy dowód.  
Odpowiedź: A = (− 6, 5),B = (9, 17),C = (− 2, 17),D = (− 11, 13) 2 2 2 2 2 2

Wersja PDF