/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 3365079

Dodaj do ulubionych
Dodaj do rozwiązanych

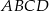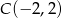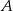W prostokącie ABCD dane są wierzchołek C (− 2 ,2 ) i wektor → AB = [3 ,3] . Wyznacz równania prostych, zawierających przekątne tego prostokąta, jeśli wiadomo, że wierzchołek A należy do prostej o równaniu x − 2y = 0 .

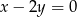Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

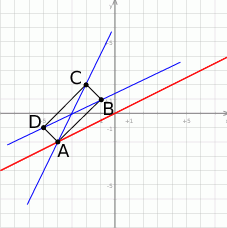
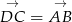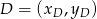Z rysunku widać, że → → DC = AB , pozwala nam łatwo wyliczyć punkt D = (xD ,yD ) :

[3,3] = [− 2 − x ,2 − y ] ⇒ D = (−5 ,−1 ). D D

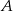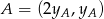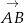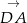Jak teraz wyznaczyć punkt A ? – wystarczy znaleźć na danej prostej taki punkt A = (2yA ,yA ) , żeby wektory → AB i → DA były prostopadłe. Liczymy

→ → 0 = AB ∘ DA = [3,3] ∘[2yA + 5,yA + 1] = 6yA + 15 + 3yA + 3 = 9yA + 1 8 yA = − 2 ⇒ A = (− 4,− 2).

Teraz beż trudu wyliczamy 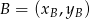B = (xB,yB) :

→ [3,3] = AB = [xB + 4,yB + 2] ⇒ B = (− 1,1).

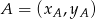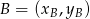Pozostało teraz napisać równania przekątnych – korzystamy ze wzoru na prostą przechodzącą przez dwa punkty: A = (xA ,yA ) i B = (xB ,yB) :

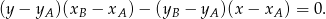
(y− yA)(xB − xA ) − (yB − yA )(x− xA) = 0.

Mamy zatem

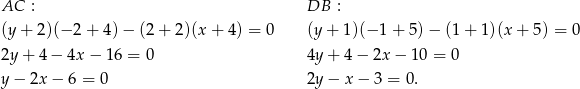
AC : DB : (y+ 2)(− 2+ 4)− (2+ 2)(x+ 4) = 0 (y+ 1)(− 1+ 5)− (1 + 1)(x + 5) = 0 2y + 4 − 4x − 16 = 0 4y+ 4− 2x − 10 = 0 y− 2x − 6 = 0 2y− x− 3 = 0.

 
Odpowiedź: AC : y − 2x − 6 = 0 DB : 2y− x− 3 = 0

Wersja PDF