Zadanie nr 3508398
Jeden bok kwadratu opisanego okręgu o równaniu 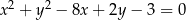 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 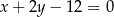 . Oblicz współrzędne wierzchołków tego kwadratu.
. Oblicz współrzędne wierzchołków tego kwadratu.
Rozwiązanie
Przekształćmy najpierw równanie okręgu tak, aby zobaczyć jaki jest jego środek i promień.
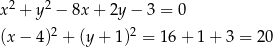
Jest to więc okrąg o środku 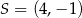 i promieniu
i promieniu 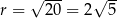 . Szkicujemy tę sytuację.
. Szkicujemy tę sytuację.
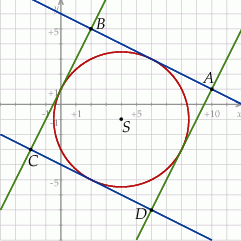
Jeżeli przyjmiemy oznaczenia wierzchołków kwadratu jak na rysunku, to zaczniemy od napisania równań prostych 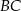 i
i 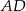 . Każda z nich jest prostopadła do danej prostej, więc mają równania postaci
. Każda z nich jest prostopadła do danej prostej, więc mają równania postaci
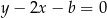
Współczynnik 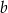 wyznaczymy sprawdzając, kiedy odległość tej prostej od punktu
wyznaczymy sprawdzając, kiedy odległość tej prostej od punktu 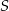 jest równa
jest równa 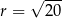 . Korzystamy ze wzoru na odległość punktu
. Korzystamy ze wzoru na odległość punktu 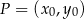 od prostej
od prostej 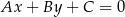 :
:
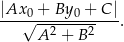
W naszej sytuacji mamy zatem
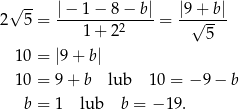
Proste 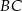 i
i 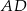 mają więc odpowiednio równania:
mają więc odpowiednio równania: 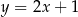 i
i 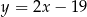 . Wyznaczamy teraz współrzędne punktów
. Wyznaczamy teraz współrzędne punktów 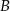 i
i 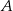 . Najpierw punkt
. Najpierw punkt 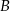 – czyli punkt wspólny prostych
– czyli punkt wspólny prostych 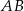 i
i 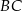 .
.
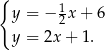
Odejmujemy od drugiego równania pierwszego i mamy
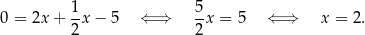
Stąd 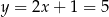 i
i 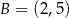 .
.
Dokładnie w ten sam sposób wyznaczmy współrzędne punktu 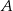 .
.
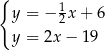
Odejmujemy od drugiego równania pierwsze i mamy
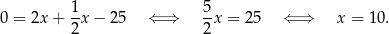
Stąd 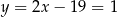 i
i 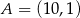 .
.
Współrzędne pozostałych dwóch wierzchołków wyznaczamy korzystając ze znajomości środka symetrii 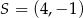 kwadratu.
kwadratu.
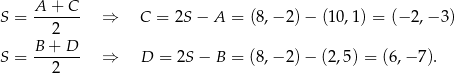
Odpowiedź: