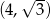/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 3553366

Dodaj do ulubionych
Dodaj do rozwiązanych

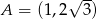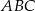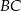Punkt √ -- A = (1,2 3) jest wierzchołkiem trójkąta równobocznego ABC . Bok BC jest zawarty w prostej o równaniu 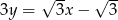√ -- √ -- 3y = 3x − 3 . Oblicz współrzędne wierzchołków B i C trójkąta.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

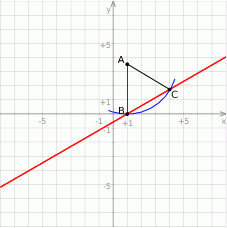
Skoro znamy współrzędne wierzchołka i równanie przeciwległego boku, możemy obliczyć długość wysokości trójkąta – jest to odległość punktu 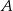A od prostej BC .

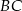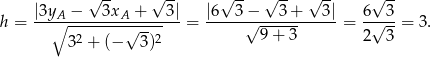
√ -- √ -- √ -- √ -- √ -- √ -- |3yA − 3xA + 3| |6 3− 3+ 3| 6 3 h = --∘----------√------ = -----√------------= -√---= 3. 32 + (− 3)2 9 + 3 2 3

Mając długość wysokości możemy wyliczyć długość boku trójkąta równobocznego.

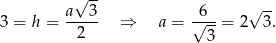
√ -- a--3- -6-- √ -- 3 = h = 2 ⇒ a = √ 3-= 2 3.

Teraz wystarczy znaleźć punkty wspólne okręgu o środku 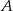A i promieniu 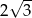√ -- 2 3 oraz danej prostej BC .

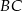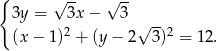
{ √ -- √ -- 3y = 3x − 3 √ -- (x− 1)2 + (y− 2 3)2 = 12.

Podstawiamy 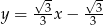√- √- y = -3-x− -3- 3 3 z pierwszego równania do drugiego.

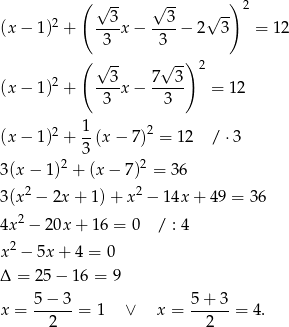
( √ -- √ -- ) 2 2 --3- --3- √ -- (x − 1) + 3 x− 3 − 2 3 = 1 2 ( ) √ 3- 7√ 3- 2 (x − 1)2 + ----x− ----- = 1 2 3 3 1 (x − 1)2 + --(x − 7)2 = 1 2 / ⋅3 3 3(x − 1 )2 + (x − 7)2 = 36 2 2 3(x − 2x + 1)+ x − 1 4x+ 49 = 36 4x 2 − 20x + 16 = 0 / : 4 2 x − 5x + 4 = 0 Δ = 25 − 16 = 9 x = 5−--3-= 1 ∨ x = 5-+-3-= 4. 2 2

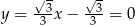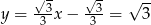Wtedy √- √- y = -33 x − 33-= 0 i √ - √ - √ -- y = -33x − -33= 3 odpowiednio. Zatem 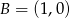B = (1,0) i √ -- C = (4, 3) .  
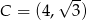Odpowiedź: 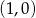(1,0) i √ -- (4, 3)

Wersja PDF