Zadanie nr 3602169
Dana jest prosta 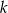 o równaniu
o równaniu 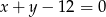 oraz punkt
oraz punkt 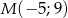 wyznacz na prostej
wyznacz na prostej 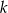 takie punkty
takie punkty 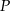 i
i 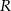 aby
aby 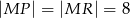 .
.
Rozwiązanie
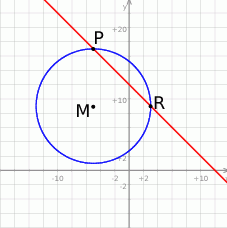
Szkicujemy sobie podaną sytuację i robi się jasne, że musimy znaleźć punkty wspólne podanej prostej i okręgu o środku 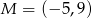 i promieniu 8.
i promieniu 8.
Równanie tego okręgu to
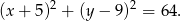
Musimy rozwiązać układ równań
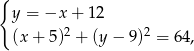
który prowadzi do równania
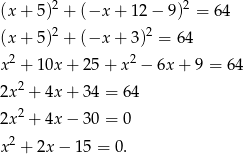
Liczymy dalej, 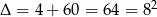 ,
, 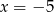 lub
lub 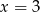 . Stąd
. Stąd 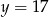 i
i 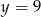 odpowiednio.
odpowiednio.
Odpowiedź: 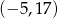 i
i