/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 3724416

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest parabola opisana równaniem 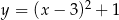2 y = (x − 3) + 1 . Tworzymy trójkąty 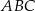ABC takie, że punkt 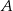A leży w początku układu współrzędnych, punkt 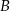B o współrzędnych 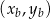(xb ,yb ) leży na paraboli, punkt 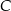C ma współrzędne (xb,0) .

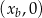  • Napisz wzór funkcji 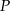P , określającej pole trójkąta 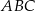ABC w zależności od 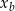xb dla xb > 0 .
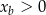  • Znajdź trójkąt o największym polu dla xb ∈ [0;2] ; w odpowiedzi podaj współrzędne punktu C .

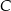Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

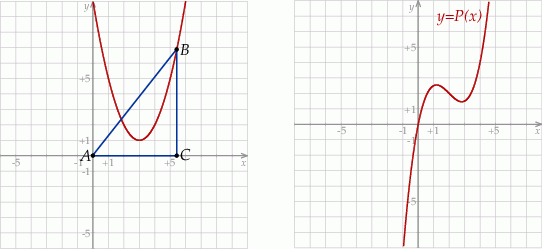
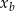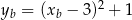  • Z obrazka widać, że otrzymany trójkąt jest prostokątny i jego przyprostokątne mają długości x b i y = (x − 3)2 + 1 b b (tutaj jest ważne, że 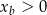xb > 0 ). Zatem wzór na pole jest następujący
    1 1 1 1 P (xb) = --xbyb = -xb[(xb− 3 )2+ 1] = --xb[x2b− 6xb + 10 ] = -x3b − 3x2b+ 5xb. 2 2 2 2

     
    Odpowiedź: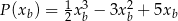 1 3 2 P(xb ) = 2xb − 3x b + 5xb

  • Aby znaleźć ekstrema na podanym przedziale liczymy pochodną
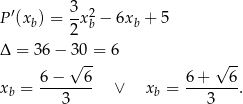
    ′ 3- 2 P (xb) = 2 xb − 6xb + 5 Δ = 36− 30 = 6 √ -- √ -- 6-−---6- 6-+---6- xb = 3 ∨ xb = 3 .

    Drugi z tych punktów jest poza podanym przedziałem, a funkcja 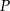P rośnie na przedziale 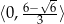√- ⟨0, 6−-36-⟩ (pochodna dodatnia) oraz maleje na przedziale 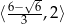6−-√6- ⟨ 3 ,2 ⟩ (pochodna ujemna). Zatem wartość największa na 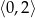⟨0,2⟩ to √- f( 6−-6-) 3 .  
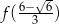    Odpowiedź: 6− √6 C = (--3--,0)

Wersja PDF