Zadanie nr 3753025
Napisz równanie wysokości trójkąta o wierzchołkach 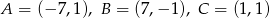 opuszczonej z wierzchołka
opuszczonej z wierzchołka 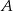 .
.
Rozwiązanie
Możemy zacząć od szkicowego rysunku.
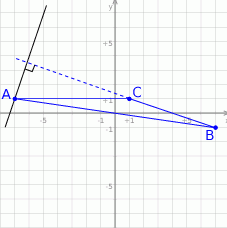
Rysunek jest trochę podchwytliwy, bo trójkąt jest rozwartokątny, ale niczego to nie zmienia: wysokość to prosta przechodząca przez wierzchołek 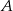 i prostopadła do prostej zawierającej bok
i prostopadła do prostej zawierającej bok 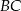 .
.
Sposób I
Zadanie jest bardzo łatwe, jeżeli skorzystamy ze wzoru na równanie prostej prostopadłej do wektora ![→v = [p ,q]](https://img.zadania.info/zad/3753025/HzadR3x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 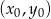 :
:
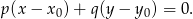
W naszej sytuacji mamy wektor ![→ → v = BC = [−6 ,2]](https://img.zadania.info/zad/3753025/HzadR6x.gif) i punkt
i punkt 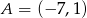 . Zatem równanie wysokości jest następujące:
. Zatem równanie wysokości jest następujące:
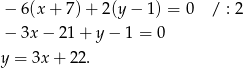
Sposób II
Jeżeli nie chcemy korzystać ze wzoru z wektorem, to piszemy najpierw równanie prostej 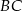 . Wstawiając do równości
. Wstawiając do równości 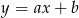 współrzędne punktów
współrzędne punktów 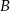 i
i 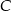 otrzymujemy układ równań.
otrzymujemy układ równań.
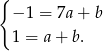
Odejmując od pierwszego równania drugie (żeby skrócić 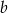 ), mamy
), mamy
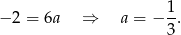
Zatem szukana wysokość będzie miała współczynnik kierunkowy 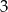 (bo jest prostopadła do
(bo jest prostopadła do 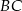 ). Szukamy więc prostej postaci
). Szukamy więc prostej postaci 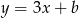 . Współczynnik
. Współczynnik 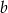 wyliczamy podstawiając współrzędne punktu
wyliczamy podstawiając współrzędne punktu 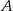 .
.

Odpowiedź: