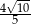/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 3758653

Dodaj do ulubionych
Dodaj do rozwiązanych

Okrąg o równaniu 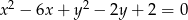2 2 x − 6x+ y − 2y+ 2 = 0 i prosta 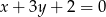x + 3y + 2 = 0 przecinają się w punktach 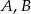A ,B . Wyznacz długość cięciwy 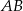AB tego okręgu.

Rozwiązanie

Z równania prostej wyznaczamy zmienną x

x = − 3y − 2

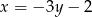
i podstawiamy do równania okręgu

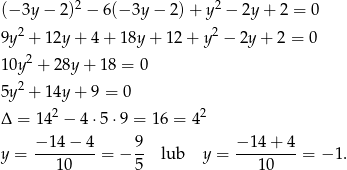
2 2 (− 3y − 2) − 6(− 3y − 2 )+ y − 2y + 2 = 0 9y 2 + 1 2y+ 4+ 18y + 12 + y2 − 2y + 2 = 0 10y 2 + 28y+ 18 = 0 2 5y + 1 4y+ 9 = 0 Δ = 142 − 4 ⋅5⋅ 9 = 16 = 4 2 y = −-14-−-4-= − 9- lub y = −-1-4+-4-= − 1. 10 5 1 0

Zatem

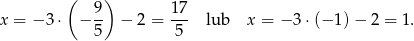
( 9) 17 x = − 3 ⋅ − -- − 2 = --- lub x = − 3⋅ (− 1 )− 2 = 1. 5 5

Stąd

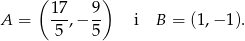
( ) A = 17-,− 9- i B = (1,− 1). 5 5

Teraz liczymy odległość między tymi punktami

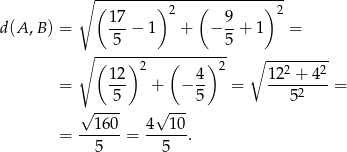
∘ -------------------------- ( )2 ( ) 2 d(A ,B ) = 17-− 1 + − 9-+ 1 = 5 5 ∘ (----)2---(----)-2 ∘ --------- 12- 4- 122-+-42- = 5 + − 5 = 52 = √ ---- √ --- --160- 4--10- = 5 = 5 .

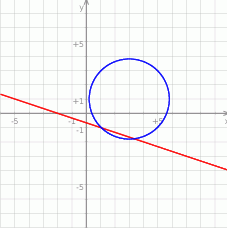
Na koniec obrazek

PIC

 
Odpowiedź: √ -- 4-510

Wersja PDF