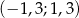/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 3778349

Dodaj do ulubionych
Dodaj do rozwiązanych

Na prostej 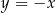y = −x wyznacz punkt, który jest równo odległy od początku układu współrzędnych oraz od punktu P = (− 2,3) .

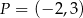Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

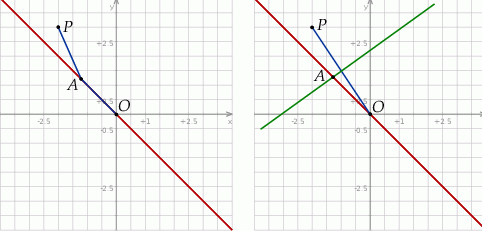
Sposób I

Szukamy punktu 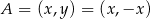A = (x,y) = (x,−x ) tak, aby spełniona była równość 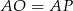AO = AP , gdzie 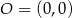O = (0,0) . Od razu porównujemy kwadraty odległości (żeby nie mieć pierwiastków).

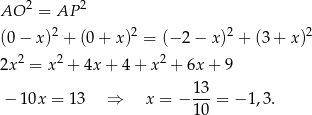
2 2 AO = AP (0 − x )2 + (0 + x)2 = (−2 − x )2 + (3 + x )2 2x 2 = x2 + 4x + 4 + x2 + 6x + 9 − 10x = 13 ⇒ x = − 13-= − 1,3. 10

Zatem 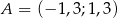A = (− 1,3;1,3) .

Sposób II

Tym razem napiszemy równanie symetralnej odcinka 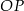OP i znajdziemy jej punkt wspólny 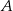A z prostą y = −x .

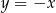Korzystając ze wzoru na równanie prostej prostopadłej do wektora → v = [p,q] i przechodzącej przez punkt (x0,y0)

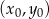
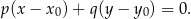
p(x − x0) + q(y − y0) = 0 .

W naszej sytuacji mamy

→ −→ v = OP = [− 2,3],

a punkt to środek odcinka 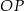OP , czyli

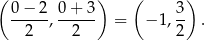
( 0− 2 0 + 3) ( 3 ) -----,------ = − 1,-- . 2 2 2

W takim razie równanie symetralnej jest następujące

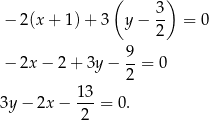
( ) − 2(x + 1)+ 3 y− 3- = 0 2 9 − 2x − 2+ 3y − --= 0 2 3y− 2x − 13-= 0. 2

Szukamy teraz punktu wspólnego tej prostej z prostą 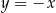y = −x , czyli podstawiamy w powyższym równaniu x = −y .

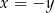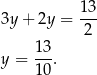
3y + 2y = 13- 2 13- y = 10.

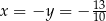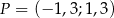Zatem x = −y = − 13 10 i P = (− 1,3;1 ,3) .  
Odpowiedź: (− 1,3;1,3)

Wersja PDF