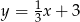Zadanie nr 3917715
Punkty 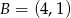 i
i 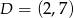 są przeciwległymi wierzchołkami rombu
są przeciwległymi wierzchołkami rombu 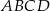 . Wyznacz równanie przekątnej
. Wyznacz równanie przekątnej 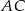 tego rombu.
tego rombu.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
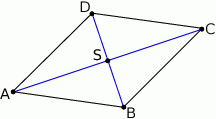
Ponieważ przekątne rombu są prostopadłe i dzielą się na połowy, równanie prostej 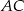 możemy napisać jako równanie prostej prostopadłej do prostej
możemy napisać jako równanie prostej prostopadłej do prostej 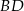 i przechodzącej przez punkt przecięcia przekątnych
i przechodzącej przez punkt przecięcia przekątnych
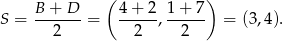
Sposób I
Napiszmy równanie prostej 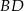 . Można to zrobić używając wzoru na równanie prostej przechodzącej przez dwa punkty, ale my poradzimy sobie bez niego. Szukamy prostej w postaci
. Można to zrobić używając wzoru na równanie prostej przechodzącej przez dwa punkty, ale my poradzimy sobie bez niego. Szukamy prostej w postaci 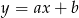 . Podstawiamy współrzędne punktów
. Podstawiamy współrzędne punktów 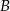 i
i 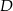
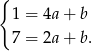
Odejmijmy od pierwszego równania drugie (żeby skrócić 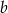 ).
).
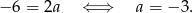
Stąd 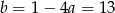 i prosta
i prosta 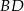 ma równanie
ma równanie 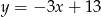 .
.
Prosta 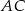 jest prostopadła do
jest prostopadła do 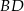 , więc musi mieć postać
, więc musi mieć postać 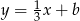 . Współczynnik
. Współczynnik 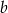 wyliczamy podstawiając współrzędne punktu
wyliczamy podstawiając współrzędne punktu 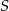 .
.
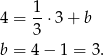
Sposób II
Tym razem skorzystamy ze wzoru na równanie prostej prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/3917715/HzadR20x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 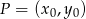
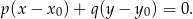
W naszej sytuacji 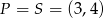 i
i
![−→ →v = BD = [− 2,6].](https://img.zadania.info/zad/3917715/HzadR24x.gif)
Prosta 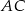 ma więc równanie
ma więc równanie
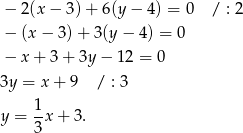
Sposób III
Zauważmy, że tak naprawdę musimy napisać równanie symetralnej odcinka 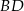 . Symetralna ta jest zbiorem punktów
. Symetralna ta jest zbiorem punktów 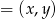 , które są równo odległe od końców odcinka. Mamy zatem
, które są równo odległe od końców odcinka. Mamy zatem
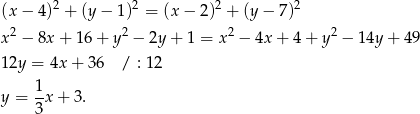
Odpowiedź: