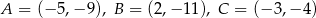Zadanie nr 3968143
Obrazem trójkąta 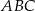 w jednokładności o środku
w jednokładności o środku 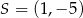 i skali
i skali 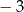 jest trójkąt
jest trójkąt 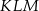 o wierzchołkach
o wierzchołkach 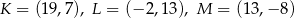 . Wyznacz współrzędne wierzchołków trójkąta
. Wyznacz współrzędne wierzchołków trójkąta 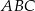 .
.
Rozwiązanie
Na początek możemy spróbować naszkicować opisaną sytuację.
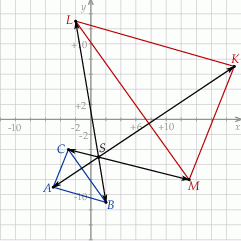
Sposób I
Z definicji jednokładności mamy równości.
![( −→ −→ ||| SK = − 3SA { −→ − → SL = − 3 SB |||( −→ −→ SM = − 3SC ( |{ [19 − 1,7 + 5] = − 3[xA − 1 ,yA + 5] ⇒ [xA − 1,yA + 5] = [−6 ,−4 ] [− 2 − 1,13 + 5] = − 3[xB − 1,yB + 5 ] ⇒ [xB − 1 ,yB + 5] = [1 ,−6 ] |( [13 − 1,− 8 + 5] = − 3[xC − 1,yC + 5] ⇒ [xC − 1,yC + 5] = [− 4,1].](https://img.zadania.info/zad/3968143/HzadR1x.gif)
Otrzymujemy stąd 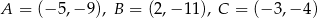 .
.
Sposób II
Jeżeli trójkąt 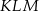 jest obrazem trójkąta
jest obrazem trójkąta 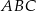 w jednokładności o środku
w jednokładności o środku 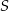 i skali
i skali 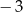 , to trójkąt
, to trójkąt 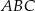 jest obrazem trójkąta
jest obrazem trójkąta 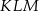 w jednokładności o tym samym środku i skali
w jednokładności o tym samym środku i skali 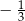 . Z definicji jednokładności mamy równości.
. Z definicji jednokładności mamy równości.
![( −→ −→ ||| SA = − 13SK { −→ − → | SB = − 13 SL ||( −→ 1 −→ SC = − 3SM ( 1 |{ [xA − 1,yA + 5] = − 3[19 − 1,7 + 5] = [− 6,− 4] [xB − 1,yB + 5 ] = − 13[− 2 − 1,13 + 5 ] = [1,− 6] |( 1 [xC − 1,yC + 5] = − 3[13− 1,− 8+ 5] = [− 4,1].](https://img.zadania.info/zad/3968143/HzadR10x.gif)
Otrzymujemy stąd 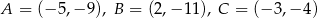 .
.
Odpowiedź: