/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 4135721

Dodaj do ulubionych
Dodaj do rozwiązanych

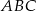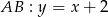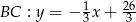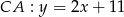Boki trójkąta ABC są zawarte w prostych o równaniach AB : y = x + 2 , BC : y = − 13x + 263 i CA : y = 2x + 11 . Wyznacz współrzędne środka okręgu opisanego na trójkącie ABC .

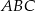Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

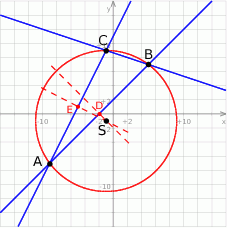
Aby wyznaczyć środek okręgu opisanego napiszemy równania dwóch symetralnych boków trójkąta 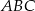ABC i znajdziemy ich punkt wspólny.

Zanim to jednak zrobimy wyznaczmy punkty wspólne podanych prostych.

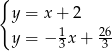
{ y = x + 2 y = − 13 x+ 236

Odejmując od pierwszego równania drugie mamy

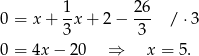
1- 26- 0 = x+ 3x + 2 − 3 / ⋅3 0 = 4x − 20 ⇒ x = 5.

Zatem 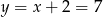y = x + 2 = 7 i B = (5 ,7) .

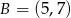Kolejne dwie proste

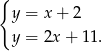
{ y = x + 2 y = 2x + 11.

Odejmujemy od drugiego równania pierwsze i mamy

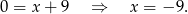
0 = x + 9 ⇒ x = − 9.

Zatem 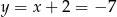y = x + 2 = − 7 i A = (− 9,− 7) .

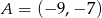Jeszcze współrzędne punktu 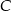C .

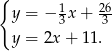
{ 1 26 y = − 3 x+ 3 y = 2x + 11.

Odejmujemy do drugiego równania pierwsze.

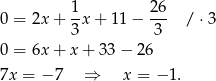
1- 26- 0 = 2x+ 3x + 1 1− 3 /⋅ 3 0 = 6x+ x+ 33 − 26 7x = − 7 ⇒ x = − 1 .

Stąd 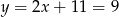y = 2x + 1 1 = 9 i C = (− 1,9) .

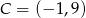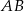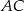Środki boków AB i AC trójkąta 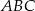ABC mają współrzędne

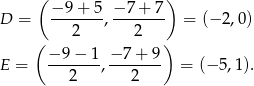
( ) −9 + 5 − 7+ 7 D = -------,------- = (− 2,0) ( 2 2 ) −-9-−-1 −7-+-9- E = 2 , 2 = (− 5,1).

Chcemy teraz napisać równanie prostej prostopadłej do 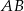AB i przechodzącej przez 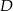D . Wiemy, że prosta 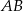AB ma współczynnik kierunkowy 1, więc prosta 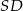SD musi być postaci 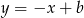y = −x + b . Współczynnik 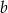b wyznaczamy podstawiając współrzędne punktu D .

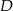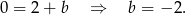
0 = 2+ b ⇒ b = − 2.

Zatem prosta 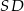SD ma równanie y = −x − 2 .

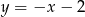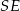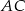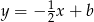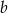Analogicznie wyznaczamy równanie symetralnej SE boku AC . Ma ona postać y = − 12x + b i b wyliczamy podstawiając współrzędne punktu E .

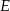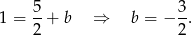
5- 3- 1 = 2 + b ⇒ b = − 2 .

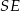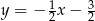Zatem prosta SE ma równanie y = − 12x − 32 .

Szukamy teraz punktu wspólnego dwóch symetralnych, czyli współrzędnych punktu 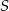S .

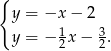
{ y = −x − 2 y = − 12x− 32.

Odejmujemy od drugiego równania pierwsze i mamy

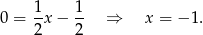
1- 1- 0 = 2x − 2 ⇒ x = − 1.

Zatem 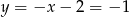y = −x − 2 = −1 i S = (− 1,− 1) .  
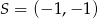Odpowiedź: (− 1,− 1)

Wersja PDF