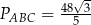/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 4145319

Dodaj do ulubionych
Dodaj do rozwiązanych

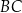Dany jest trójkąt równoboczny ABC , w którym ( 5) A = − 1, 2 . Bok BC tego trójkąta jest zwarty w prostej o równaniu 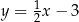y = 12x − 3 . Oblicz współrzędne środka odcinka 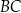BC oraz oblicz pole trójkąta ABC .

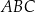Rozwiązanie

Zaczynamy od rysunku

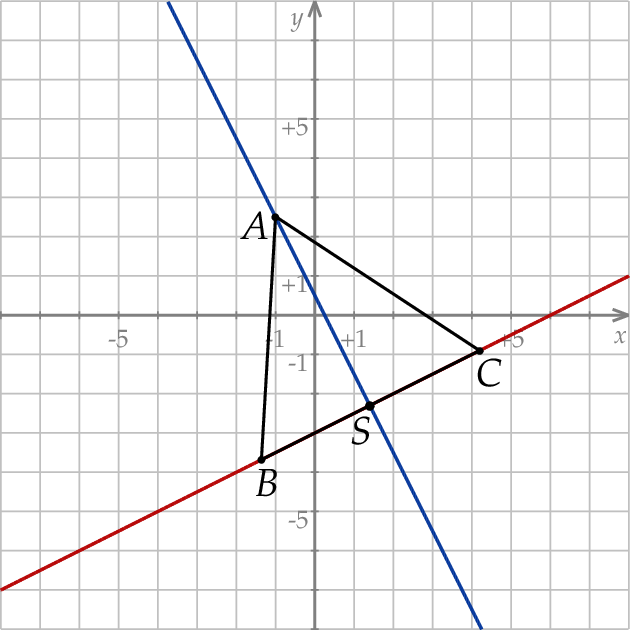
ZINFO-FIGURE

Jeżeli 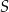S jest środkiem odcinka 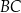BC , to prosta 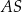AS jest jego wysokością. Jest więc prostopadła do prostej 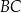BC i ma równanie postaci

y = − 2x + b.

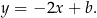
Współczynnik 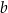b wyznaczamy podstawiając w tym równaniu współrzędne punktu A .

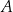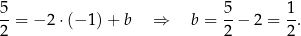
5-= − 2⋅ (−1 )+ b ⇒ b = 5-− 2 = 1. 2 2 2

Prosta 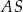AS ma więc równanie 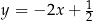1 y = − 2x + 2 i możemy wyznaczyć jej punkt wspólny 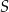S z prostą BC .

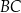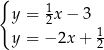
{ y = 12x − 3 1 y = − 2x+ 2

Odejmujemy od pierwszego równania drugie i mamy

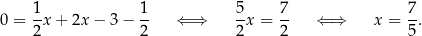
0 = 1-x + 2x − 3 − 1- ⇐ ⇒ 5-x = 7- ⇐ ⇒ x = 7. 2 2 2 2 5

Stąd

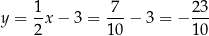
y = 1-x− 3 = -7-− 3 = − 23- 2 10 10

i 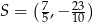( ) S = 75,− 2130 . To pozwala nam obliczyć długość wysokości trójkąta ABC .

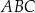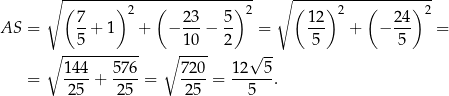
∘ (------)----(----------)--- ∘ (----)----(------)-- 7 2 23 5 2 12 2 24 2 AS = -+ 1 + − ---− -- = --- + − --- = ∘ --5-------- ∘ 10-- 2 √ -- 5 5 144 576 720 12 5 = ----+ ----= ----= ------. 2 5 25 25 5

To pozwala obliczyć długość a boku trójkąta.

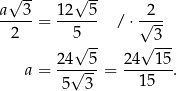
√ -- √ -- a--3- 12--5- -2-- 2 = 5 / ⋅√ -- √ -- √ 3-- 24--5- 24--15- a = √ --= 15 . 5 3

Pole trójkąta ABC jest więc równe

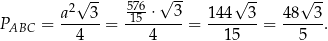
√ -- √ -- √ -- √ -- a2--3- 51756⋅--3- 144---3 48---3 PABC = 4 = 4 = 15 = 5 .

 
Odpowiedź: 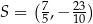S = (7,− 23) 5 10 , √- P = 48-3- ABC 5

Wersja PDF