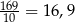/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 4234797

Dodaj do ulubionych
Dodaj do rozwiązanych

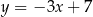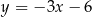Dwa boki kwadratu zawierają się w prostych o równaniach y = − 3x + 7 i y = − 3x− 6 . Oblicz pole tego kwadratu.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

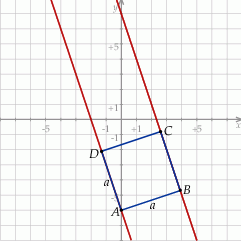
Dane proste są równoległe, więc długość boku kwadratu, o którym mowa w treści zadania, to odległość między tymi prostymi. Aby ją obliczyć, znajdujemy jakikolwiek punkt na jednej z tych prostych – np. punkt 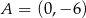A = (0,− 6) leży na drugiej prostej.

Sposób I

Piszemy teraz równanie prostej prostopadłej do danych prostych, czyli prostej postaci 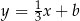y = 1x+ b 3 , która przechodzi przez A .

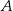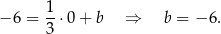
1- − 6 = 3 ⋅0 + b ⇒ b = − 6.

Szukamy teraz punktu wspólnego 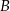B pierwszej z podanych prostych i prostej AB .

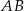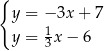
{ y = − 3x+ 7 1 y = 3x − 6

Odejmujemy od pierwszego równania drugie i mamy

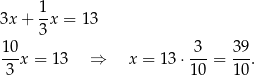
3x + 1x = 13 3 10 3 3 9 --x = 13 ⇒ x = 1 3⋅ ---= ---. 3 10 1 0

Stąd

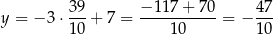
3 9 − 117 + 7 0 47 y = −3 ⋅1-0 + 7 = ----10----- = − 10-

i 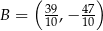( ) B = 39,− 47 10 10 . Mamy zatem

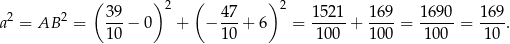
( 3 9 ) 2 ( 47 )2 1521 169 1690 169 a2 = AB 2 = ---− 0 + − ---+ 6 = -----+ ----= -----= ----. 1 0 10 1 00 100 10 0 1 0

Sposób II

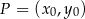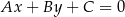Korzystamy ze wzoru na odległość punktu P = (x0,y0) od prostej Ax + By + C = 0 :

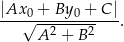
|Ax-0√-+-By-0 +-C|. A 2 + B 2

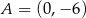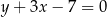W naszej sytuacji mamy liczymy odległość punktu A = (0,− 6) od prostej y + 3x − 7 = 0 .

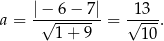
|− 6− 7| 13 a = -√--------= √----. 1 + 9 10

Pole kwadratu jest więc równe

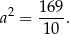
169 a2 = ---. 10

 
Odpowiedź: 169 -10 = 16 ,9

Wersja PDF