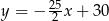/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 4280252

Dodaj do ulubionych
Dodaj do rozwiązanych

Znajdź równanie prostej 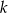k przechodzącej przez punkt 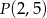P(2 ,5) , która ogranicza wraz z dodatnimi półosiami układu współrzędnych trójkąt o polu równym 36.

Rozwiązanie

Możemy zacząć od szkicowego rysunku.

PIC

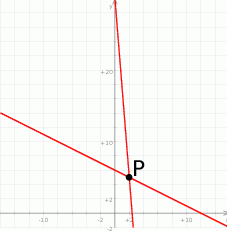
Proste przechodzące przez punkt 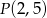P(2,5 ) możemy zapisać w postaci

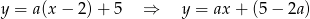
y = a(x − 2) + 5 ⇒ y = ax + (5 − 2a)

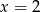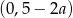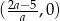(tak naprawdę to jedną pomijamy: pionową x = 2 , ale ona z pewnością nie jest odpowiedzią). Prosta ta przecina osie układu w punktach (0,5 − 2a) i (2a−-5,0) a Jeżeli punkty te mają być na dodatnich półosiach układu to musimy mieć

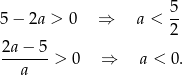
5 5 − 2a > 0 ⇒ a < -- 2 2a−--5-> 0 ⇒ a < 0. a

Otrzymany trójkąt jest prostokątny i dane pole daje nam równanie

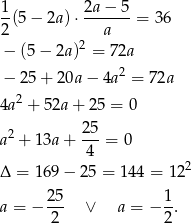
1 2a − 5 -(5 − 2a )⋅-------= 36 2 a − (5− 2a)2 = 72a 2 − 25+ 20a − 4a = 72a 4a2 + 52a + 25 = 0 a2 + 13a+ 25-= 0 4 Δ = 169− 25 = 14 4 = 122 a = − 25- ∨ a = − 1-. 2 2

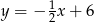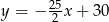
Daje to nam dwie proste: 1 y = − 2x + 6 i 25 y = − 2 x + 30  
Odpowiedź: 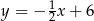1 y = − 2x+ 6 i 25 y = − -2 x + 3 0

Wersja PDF