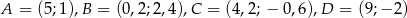/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 4284516

Dodaj do ulubionych
Dodaj do rozwiązanych

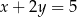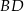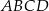Prosta o równaniu x + 2y = 5 zawiera przekątną BD rombu ABCD , którego bok ma długość 5. Wyznacz współrzędne wierzchołków rombu jeżeli A = (5,1) .

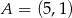Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

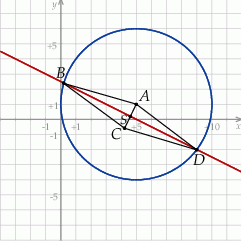
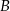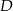Aby wyznaczyć współrzędne wierzchołków B i D szukamy punktów wspólnych podanej prostej i okręgu o środku 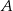A i promieniu 5, czyli okręgu o równaniu

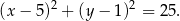
(x − 5)2 + (y − 1)2 = 25.

Podstawiamy w tym równaniu 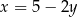x = 5 − 2y .

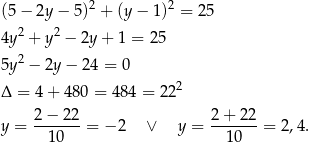
(5− 2y− 5)2 + (y− 1)2 = 25 4y2 + y2 − 2y + 1 = 25 2 5y − 2y − 24 = 0 Δ = 4+ 4 80 = 484 = 222 y = 2-−-22-= − 2 ∨ y = 2+--22-= 2 ,4 . 10 10

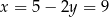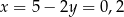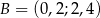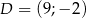Stąd odpowiednio x = 5 − 2y = 9 i x = 5 − 2y = 0,2 . Zatem B = (0,2;2,4) i D = (9;− 2) . Współrzędne wierzchołka 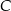C obliczymy korzystając z tego, że przekątne rombu dzielą się na połowy. Punkt 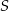S przecięcia się przekątnych ma współrzędne

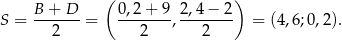
( ) B + D 0,2+ 9 2,4 − 2 S = ---2---= ---2---,---2---- = (4,6;0,2).

Z drugiej strony punkt 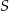S to także środek odcinka 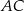AC , więc

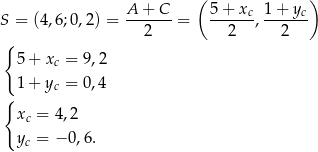
A + C ( 5+ x 1 + y ) S = (4,6 ;0,2) = -------= -----c,-----c { 2 2 2 5 + x = 9,2 c 1 + yc = 0,4 { xc = 4 ,2 yc = − 0,6.

Zatem 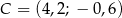C = (4,2; − 0,6) .  
Odpowiedź: A = (5;1),B = (0,2;2,4),C = (4,2; − 0,6),D = (9;− 2)

Wersja PDF