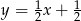/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 4322155

Dodaj do ulubionych
Dodaj do rozwiązanych

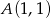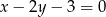Zapisz równanie prostej przechodzącej przez punkt A (1,1) i równoległej do prostej danej równaniem x − 2y − 3 = 0 .

Rozwiązanie

Podane równanie prostej możemy zapisać w postaci kierunkowej (wyliczamy 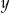y )

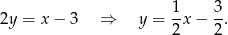
2y = x − 3 ⇒ y = 1x − 3. 2 2

Prosta równoległa do tej prostej ma ten sam współczynnik kierunkowy, jest zatem postaci 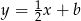y = 12x + b . Współczynnik 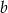b wyliczamy z faktu, że ma na niej leżeć punkt 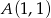A (1,1) (wstawiamy go do równania).

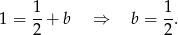
1 = 1-+ b ⇒ b = 1-. 2 2

 
Odpowiedź: y = 1x + 1 2 2

Wersja PDF