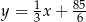Zadanie nr 4341208
Przekątne rombu 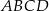 przecinają się w punkcie
przecinają się w punkcie 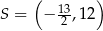 . Punkty
. Punkty 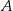 i
i 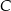 leżą na prostej o równaniu
leżą na prostej o równaniu 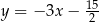 . Wyznacz równanie prostej
. Wyznacz równanie prostej 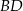 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
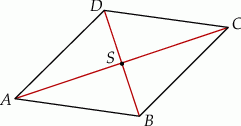
Ponieważ przekątne rombu są prostopadłe więc prosta 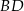 jest prostopadła do
jest prostopadła do 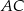 , czyli jest to prosta postaci
, czyli jest to prosta postaci 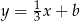 . Współczynnik
. Współczynnik 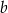 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 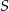 .
.
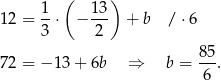
Zatem przekątna  ma równanie:
ma równanie: 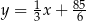 .
.
Odpowiedź: