/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 4425383

Dodaj do ulubionych
Dodaj do rozwiązanych

W kwadracie 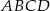ABCD dane są wierzchołek 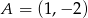A = (1,− 2) i środek symetrii 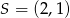S = (2,1) . Oblicz pole kwadratu ABCD .

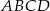Rozwiązanie

Jeżeli naszkicujemy obrazek,

PIC

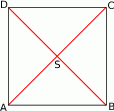
to widać, że długość odcinka 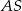AS to połowa długości przekątnej kwadratu.

Sposób I

Jeżeli oznaczymy długości boku kwadratu przez a to mamy równość.

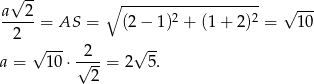
√ -- a 2 ∘ ------------------- √ --- -----= AS = (2 − 1)2 + (1+ 2)2 = 10 2 √ --- √ -- a = 10 ⋅√2--= 2 5. 2

Zatem pole jest równe

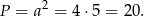
P = a2 = 4 ⋅5 = 20.

Sposób II

Podobnie jak poprzednio liczymy

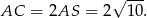
AC = 2AS = 2√ 10.

tym razem skorzystamy jednak ze wzoru na pole z przekątnymi

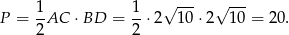
1 1 √ --- √ --- P = 2AC ⋅BD = 2-⋅2 1 0⋅2 1 0 = 20.

 
Odpowiedź: 20

Wersja PDF